机器学习笔记
机器学习
小小的俗称一波deeplearning，仅以此文作为笔记，参考课程：
https://www.bilibili.com/video/BV1Pa411X76s?p=66&vd_source=b5a5a804f02900e9715541fac229a727
本文暂不记录任何代码实现，仅记录我对于机器学习过程的直观理解。
0x01 第一课 机器学习入门
机器学习分为有监督和无监督学习
- 有监督学习是输入时就有结果的学习过程
- 无监督是输入一大堆，让机器自行分类的过程
一、线性回归
输入一大堆数据，通过线性拟合将其趋向整合为一个方程。
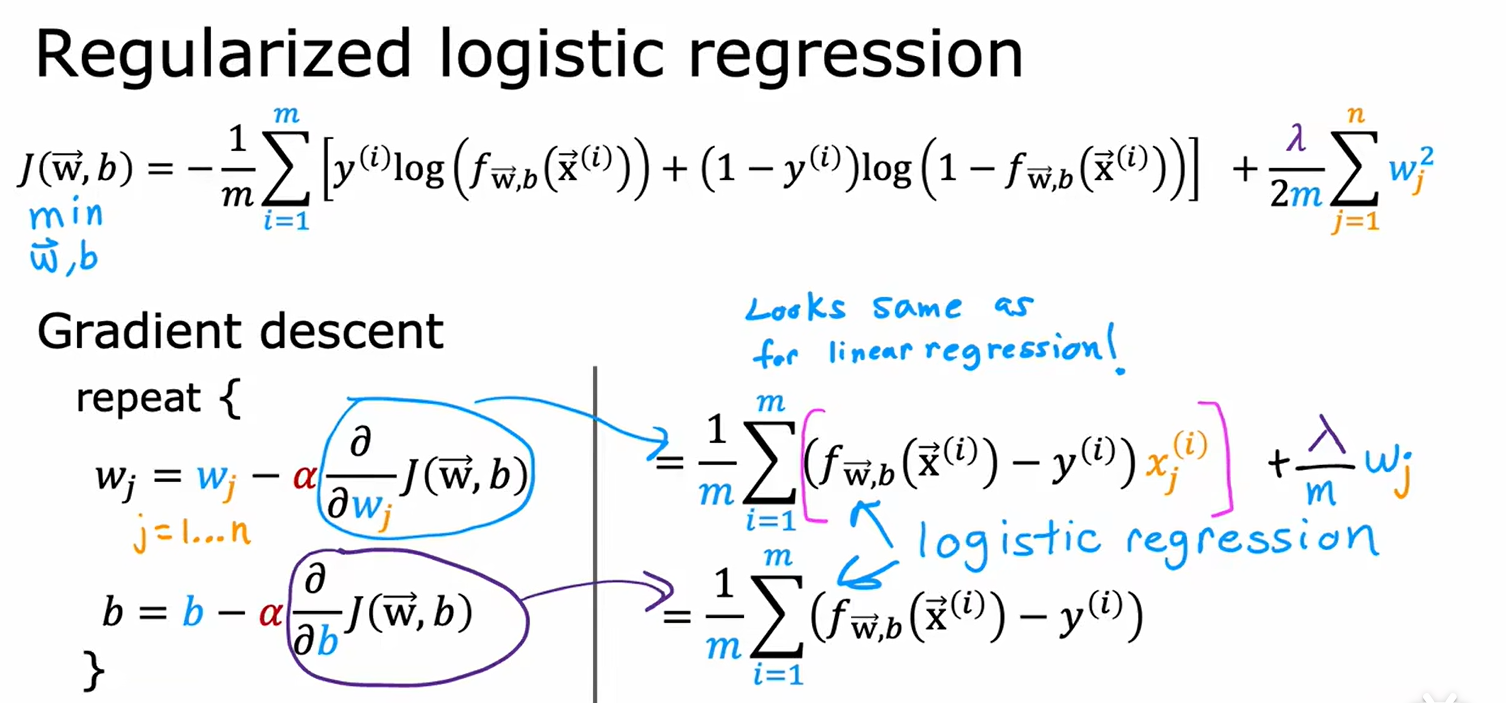
输入由x1,x2…xn,y组成的数据集，通过随机初始化w1,w2….wn，使得这一拟合出的直线与样本集的差距尽量小，其差距由代价函数（cost function）量化，如上所示。我们的目标就是不断调整w和b的取值，使得代价函数最小。
注：上图中m为样本数量。
这里提到两个概念，代价函数和损失函数，其中代价函数用 J(w,b) 表示，用于表示整个样本集和当前拟合出曲线的差距。而损失函数 ，用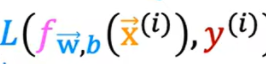
表示，用于代表一个样本所造成的偏差值大小。其中代价函数被定义为所有样本点损失函数的平均值再除以2。
1、梯度下降
要达成上述目地，我们需要逐步调整w和b的值，同过如下的方式：
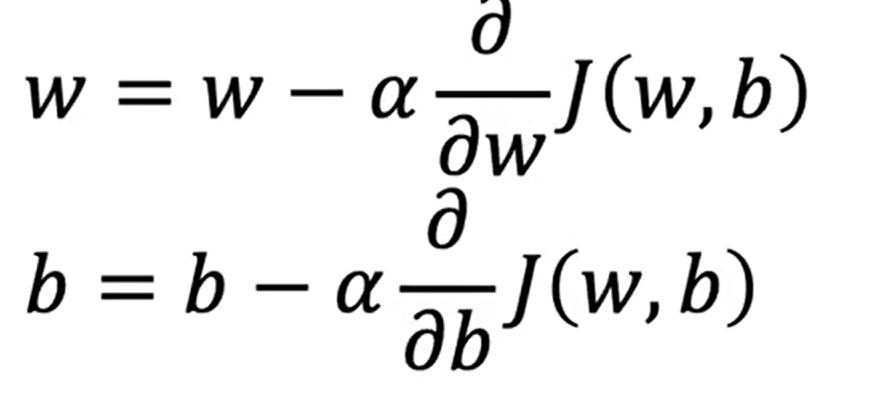
其中，等式右侧的的右侧的 值实际就是对代价函数求导，来判断在这一点上w、b的梯度值，直观来说，就是在这一点的下降趋势是否陡峭。若陡峭（且为正），则w就会随着上面的方程式快速减少），可以用如下的图示进行直观理解：
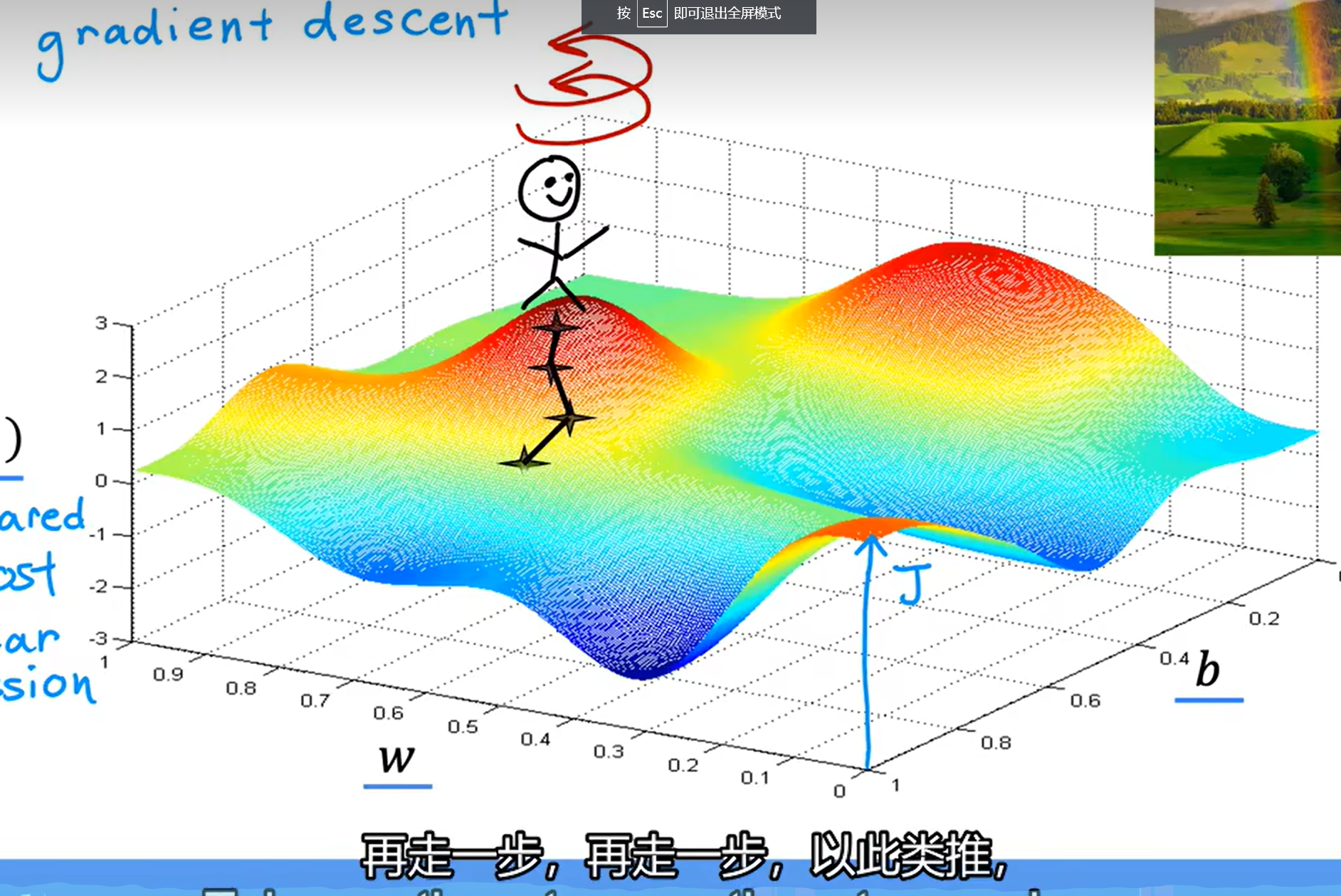
假设函数只有一个w（因为三维比较好理解），代价函数为纵轴，梯度下降所做的就是找到一条更快速下山的路线，若比较陡峭，就一步多走一点，若比较平缓，则少走一点。总之就是判断斜率然后判断以多大的速度往哪边走，但是要衡量走路的速度值，我们需要有一个基准数，也就是上式中的学习率a。
2、学习率
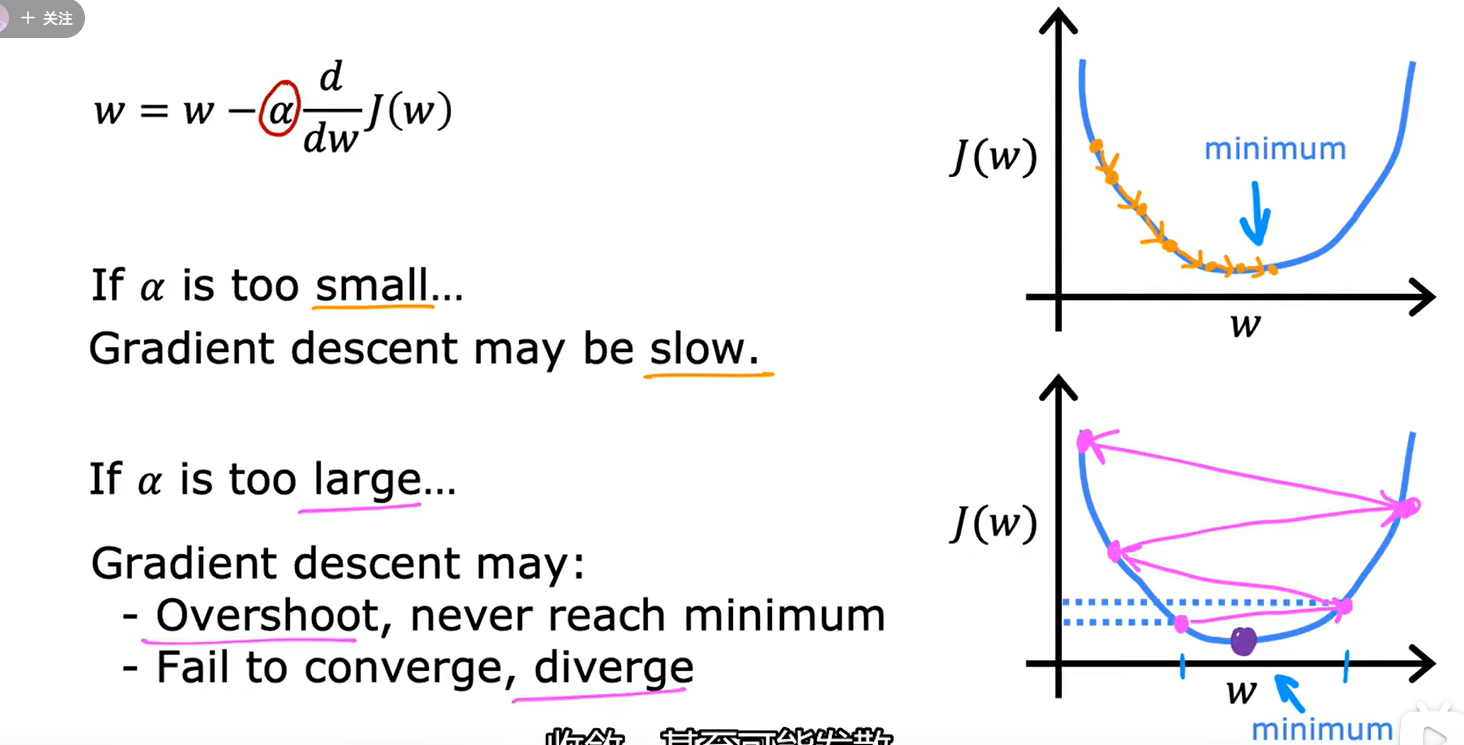
如图所示，a若选择的太小，如上图右上所示，梯度下降的进行过程就太慢。反之如果a选择的过大，可能导致梯度下降永远无法进行到最小值点。
3、线性回归的梯度下降
在线性回归下，即我们使用线性回归的代价函数，我们可以将其代价函数与梯度下降算法合并，得到以下算式：
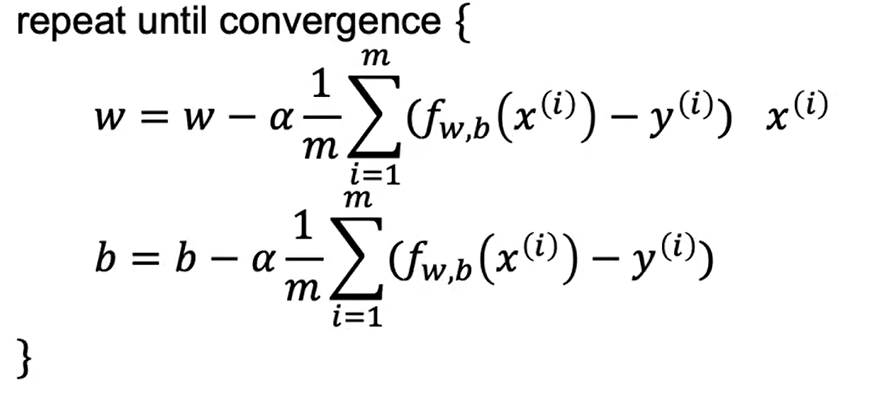
只要反复对初始化过的w和b执行如上操作，待w和b的值趋于不变时，我们就求出了完美的w和b。然后带入原算式 y=wx+b，就可以根据输入的x算出任意y的值。
要判断梯度下降是否收敛，可以观察 训练次数-损失函数 曲线，如下所示。
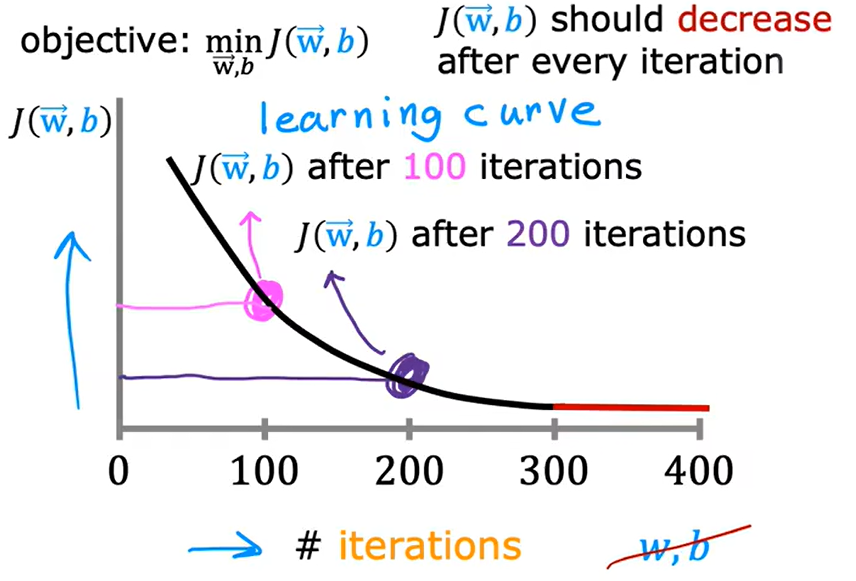
通过梯度下降是否收敛，可以反映出学习率的选用是否合适，一般来说，学习率以三倍为一缩放，十倍为两缩放。即0.1、0.3、1.0、3.0、10、30、100这样的速率进行调整。
4、向量化
实际情况下，不可能w（属特征值）只有一个，肯定y是有一大堆wx组成的，因此可用向量化表示如下：
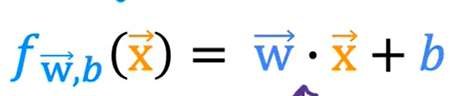
向量化的好处就是，我们可以直接使用点乘这一运算计算大量数据的乘法，最终，其梯度下降算法如下所示：
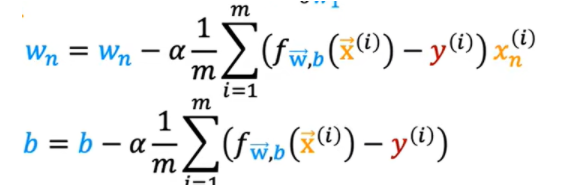
二、特征缩放
1、为什么要进行特征缩放？
在线性回归问题中，假设由两个特征，这两个特征的基础值相差较大，如一个在0-1范围内，另一个在10-1M范围内，若我们画出其取值分布图，其将如下图左上所示，当我们如右上画出其代价函数等高线时，其将会是非常瘦长的，因为相对来讲，左图x2对其影响很大，而x1对其影响很小。
假如假设x1和x2对最终的y值起到几乎同等作用的印象，那么x1>>x2就会导致w1<<w2的结果，又因为二者共享同一个学习率，因此在进行梯度下降时，梯度曲线极有可能在对w1进行缩放时左右横跳，同时若将a设置的太小，又会对w2影响太小导致训练缓慢。因此我们需要对x1、x2进行缩放。
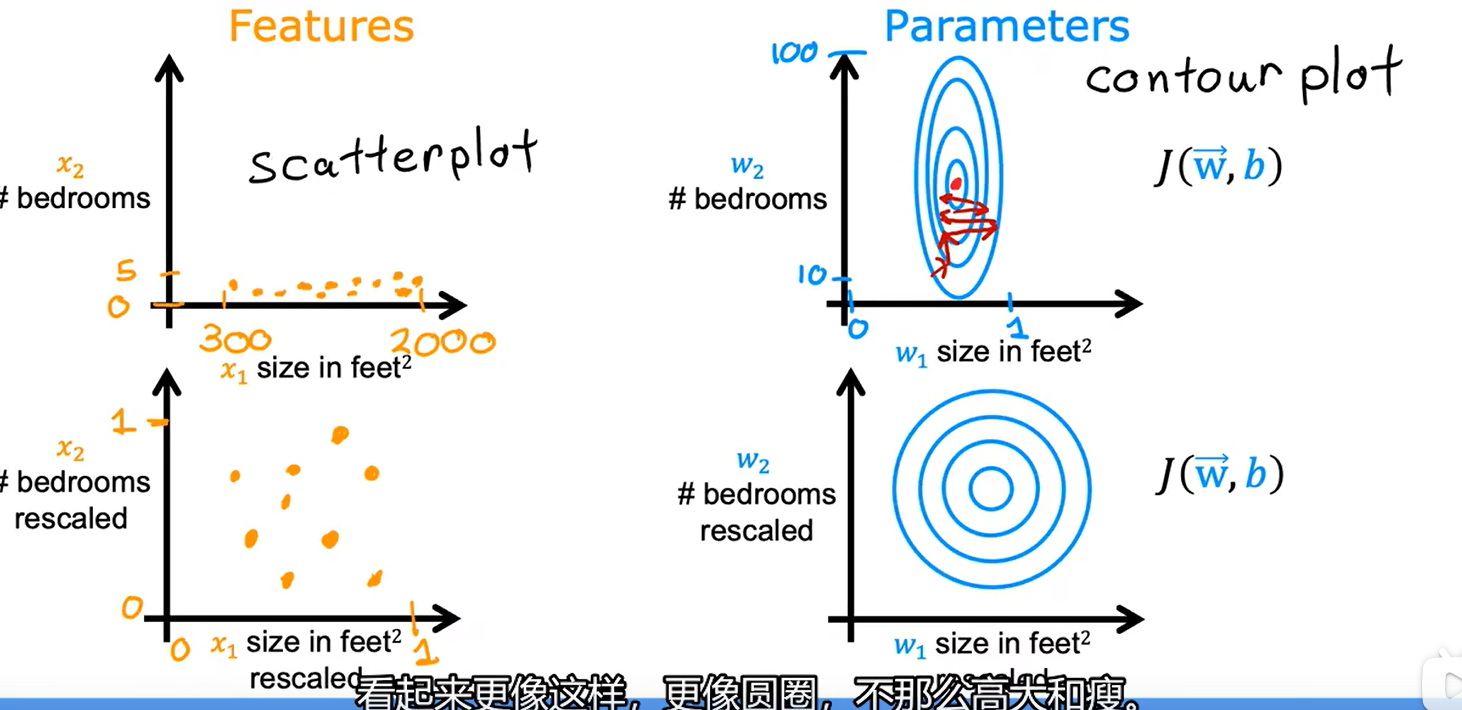
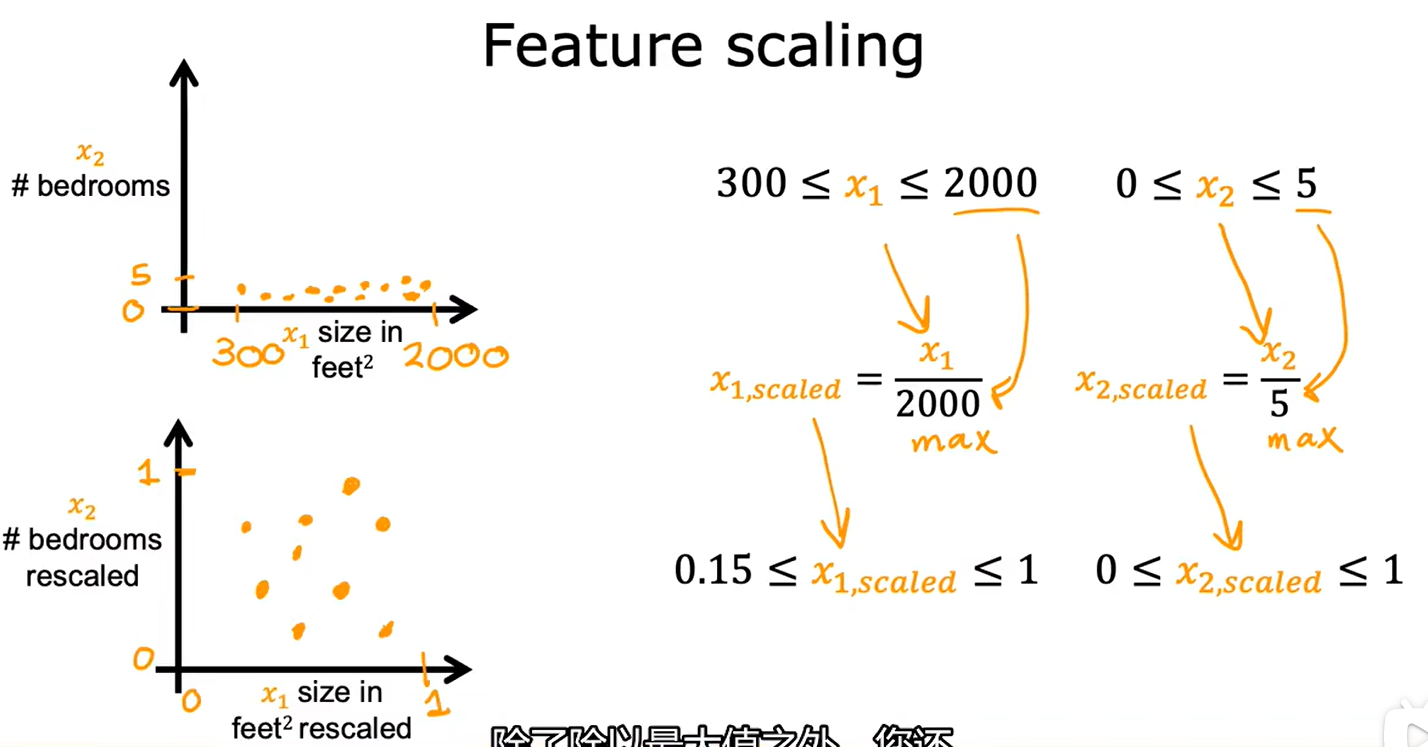
2、如何进行特征缩放？
基于最大值进行特征缩放
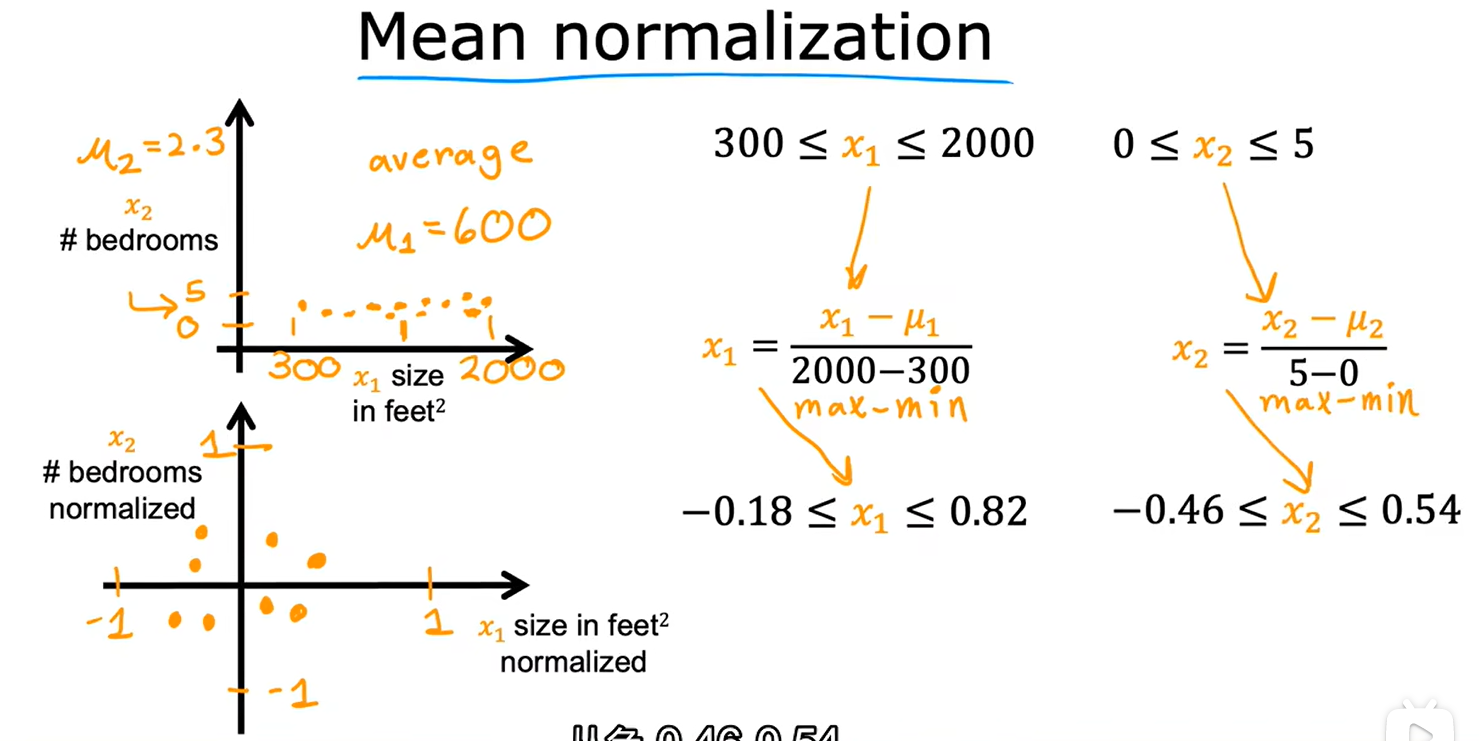
基于平均值进行特征缩放（均值归一化）
其中μ为x的平均值。
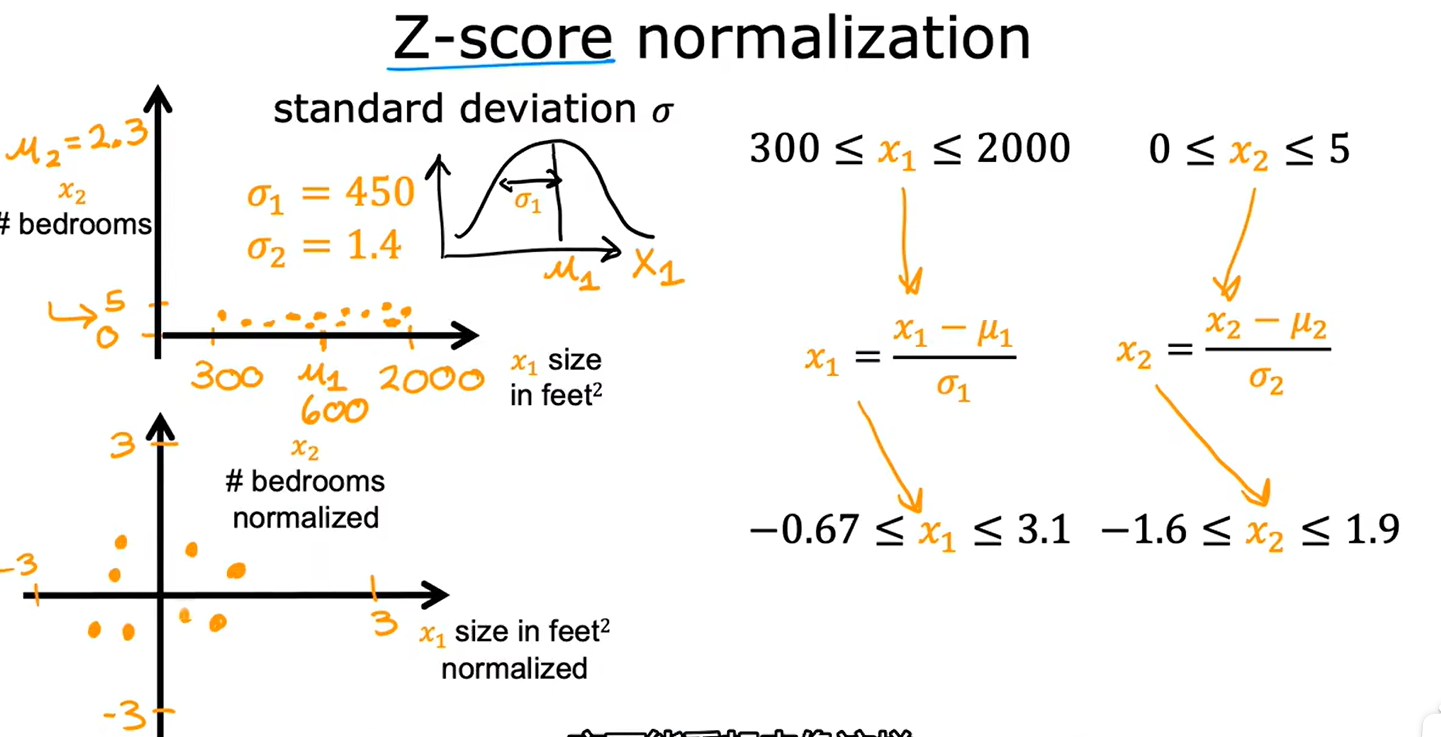
基于正态分布进行特征缩放
其中μ为x平均值，σ为标准差。
三、逻辑回归
逻辑回归用于根据给定的特征，将对样本进行二分类。
1、线性回归不再合适的原因
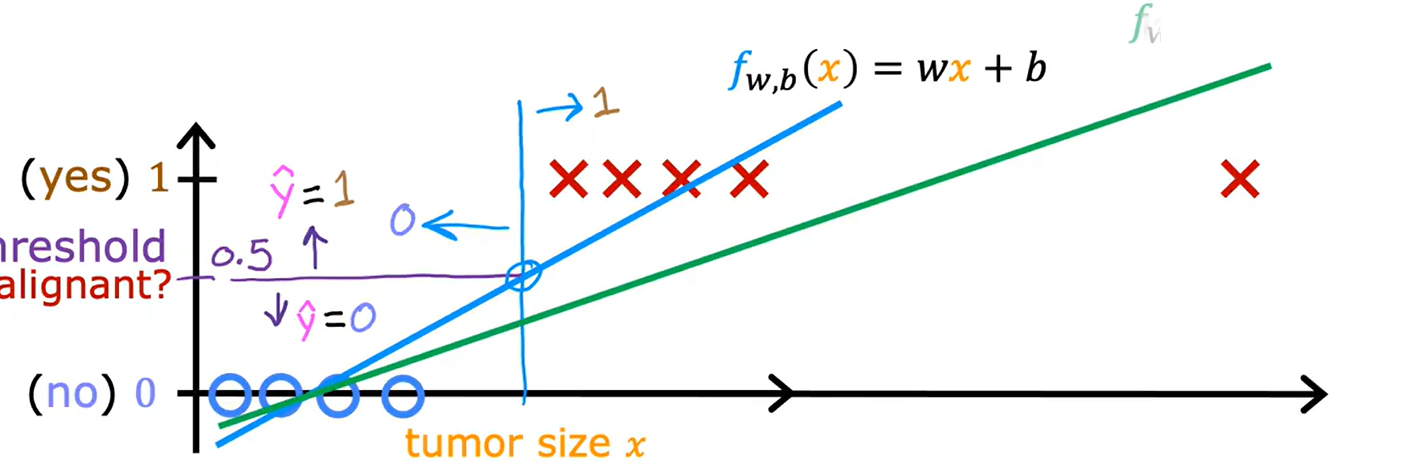
由于可能会有特别离谱的样本值，可能会把拟合出的线拉飞。
2、逻辑回归详解
逻辑回归沿用但不完全沿用线性回归：
损失函数如下：
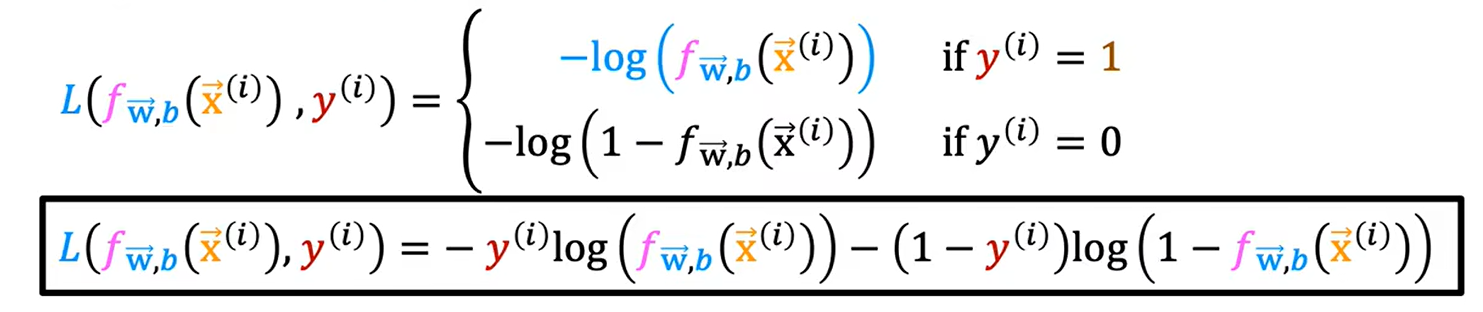
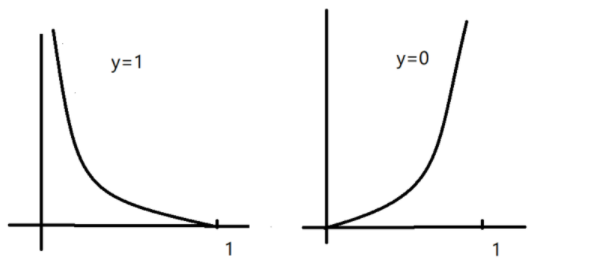
上式和下式是同一个意思，从主观上理解，当y等于1时，求出的值越远离1，也就是越靠近零，说明误差越大；反之越靠近1则误差越小，因此，上述两曲线应分别如下图所示。
通过以上损失函数，可累加轻易知代价函数如下：
通过次代价函数，可进一步推出其梯度下降公式如下(分别求偏导数乘以学习率)：
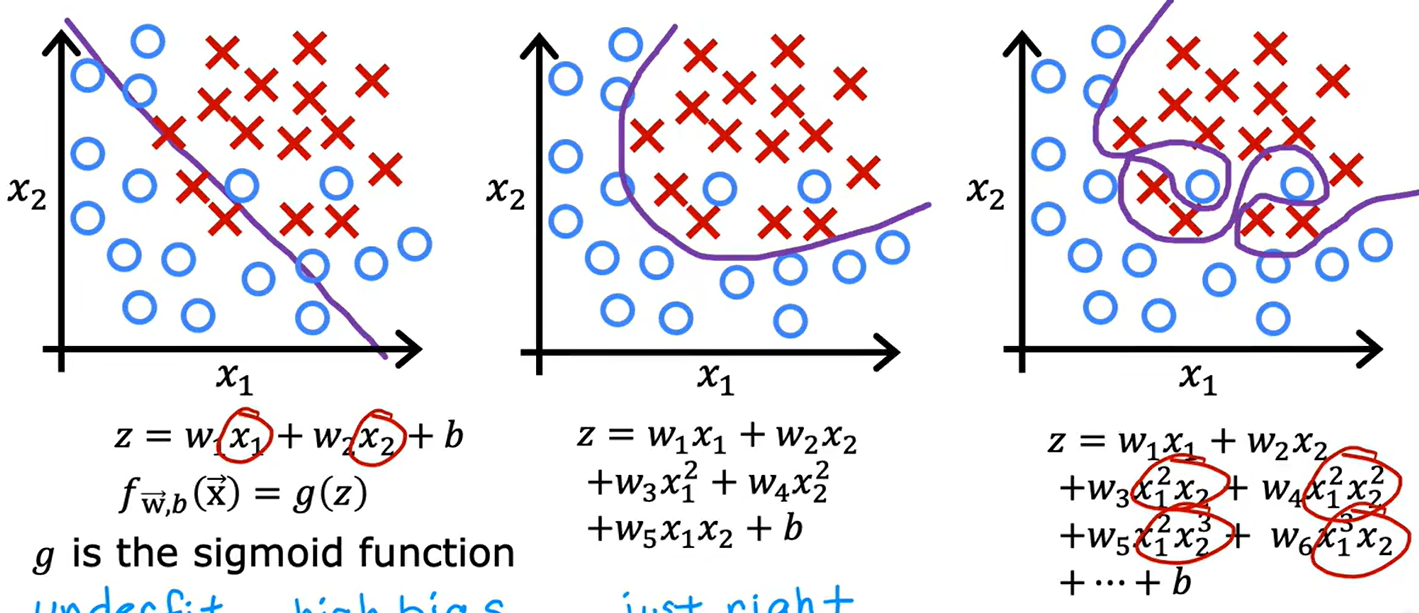
3、过拟合（高方差）
当一条曲线和数据集的契合程度高，我们成为其拟合程度好。比如如下第二条条曲线，由于我们对x进行了多项式操作，使得其拟合程度相较单纯的线性回归，也就是第一条曲线，拟合度变得更高了。
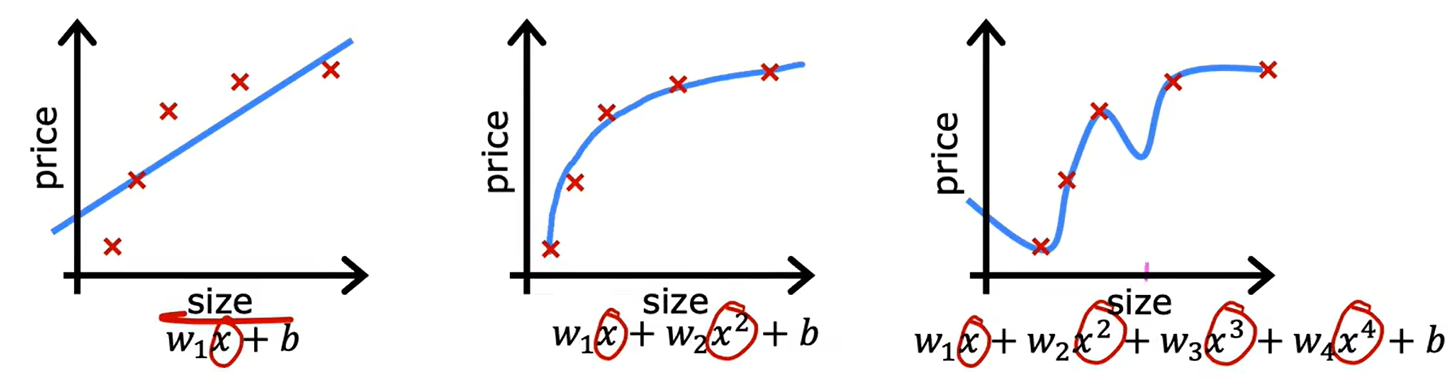
然而在第三条曲线中，我们添加了过多的多项式，使得曲线完全符合样本点，导致了过拟合现象。在过拟合现象发生后，一旦样本有轻微变化，样本曲线就会发生巨大的改变，且其预测效果也不好。如下，逻辑回归中也可能会出现过拟合现象：
解决过拟合有三种方式：
- 增加样本量
- 在样本量较少的情况下，精简单个样本的特征数量
- 正则化
其中方式一有点在于简单好用，但是我们可能没有更多样本；方式二可以解决问题，但是会损失我们掌握的信息；方式三是方式二的更好版本，也是一种较为科学的解决方案；
正则化详解
正则化的核心思想是缩小特征的系数，也就是缩小w的值（尤其是高维度特征的w）。
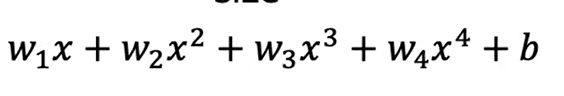
如对于上式而言，我们应尽量使得w3、w4趋近于0，也就是尽量小。因此，我们将引入一种对于参数的惩罚机制，这一惩罚机制通过修改代价函数达成。
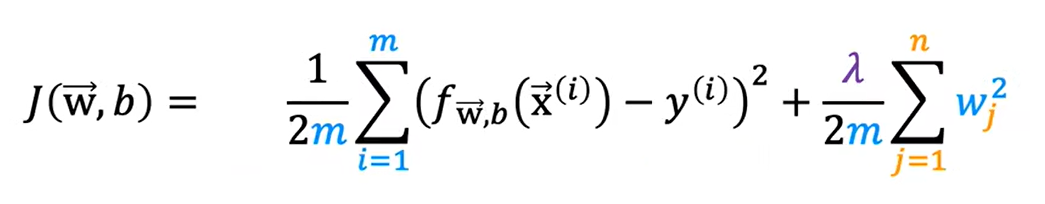
源本代价函数仅仅是损失函数的平均值除以2，在进行正则化时，代价函数如上所示。若出现极大的w，会使得代价函数随之变大，这就会使得w在每一轮的迭代中尽量变小。其中λ制定了正则化的速度。
进一步的，我们对于代价函数的修改就会体现在梯度下降的过程中，如线性回归的梯度下降会变成如下形式，逻辑回归也是类似的：
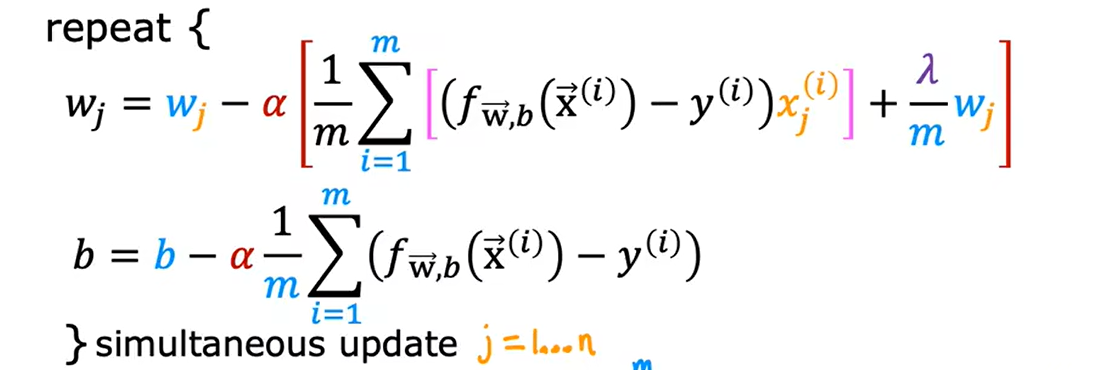
逻辑回归的正则化：
0x02 第二课 机器学习拓展
一、神经网络的使用
无论是线性回归、多项式回归还是逻辑回归，当模型训练好后，都是输入->计算->输出的模型，然而在真正解决问题时，人类的神经元往往是多层的，同时线性会非线性的混用也可以增加思考的层次，因此，我们要将多个回归模型串起来。
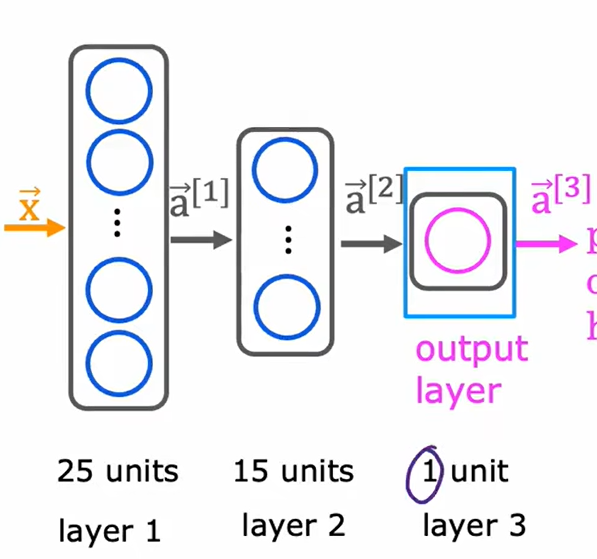
如上图所示，这是一个三层的神经网络，第一层有二十五个单元，第二层有十五个单元，第三层有一个单元。我们要定义整个网络中的某个回归模型，如第一层第2个模型的w，使用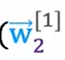
来进行表示。每个单元均对应多个输入和一个输出。
不考虑w、b参数的训练过程，假设我们已经训练好了，要使用此网络，在每一层代码所做的事应该如下所示：
1 | def my_dense(a_in, W, b, g): |
我们可以使用矩阵操作将其简化：
1 | def dense(A_in,W,B): |
对于激活函数的选取：
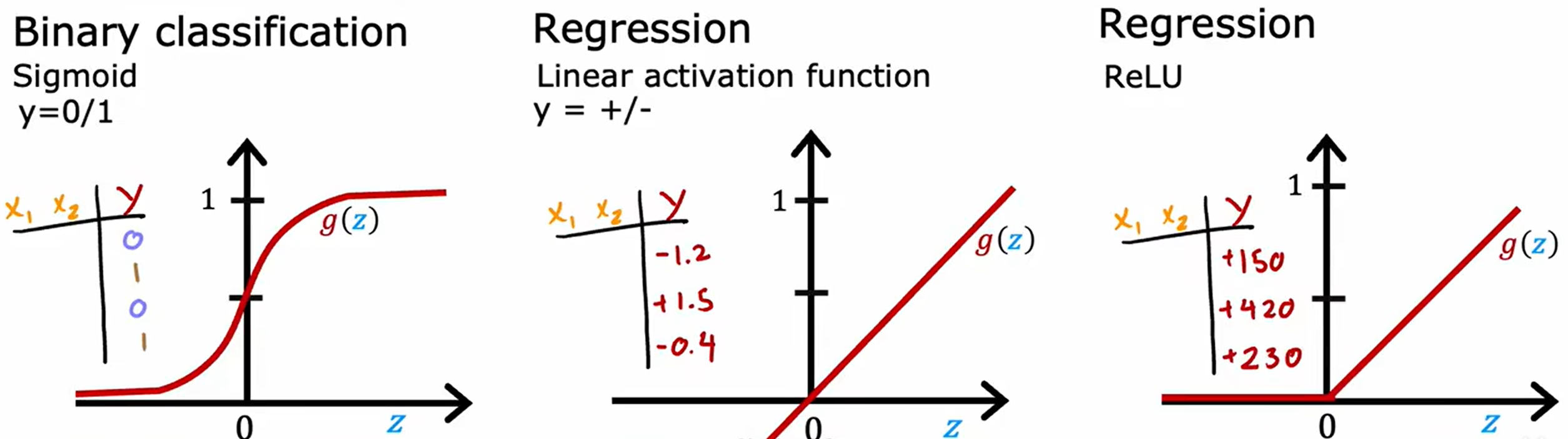
二元分类取第一个也就是 1/(e^z+1) ；评估升降取第二个；预测价格取第三个。
选择激活函数的核心就是引入非线性，因为如果一个神经网络内部全都是使用的线性回归模型，那其本质就是一个线性回归模型，可用多项式展开来证明这一说法。
二、Softmax
1、模型介绍
上述内容中，我们使用了逻辑回归解决二分类问题，但是未解决多元分类问题。沿用逻辑回归的思路和算算式，我们可以将其拓展为多元分类问题的解决思路。
先用sigmoid方式依次求出值，然后取比例大小即可，没有什么新意。损失函数如下所示：
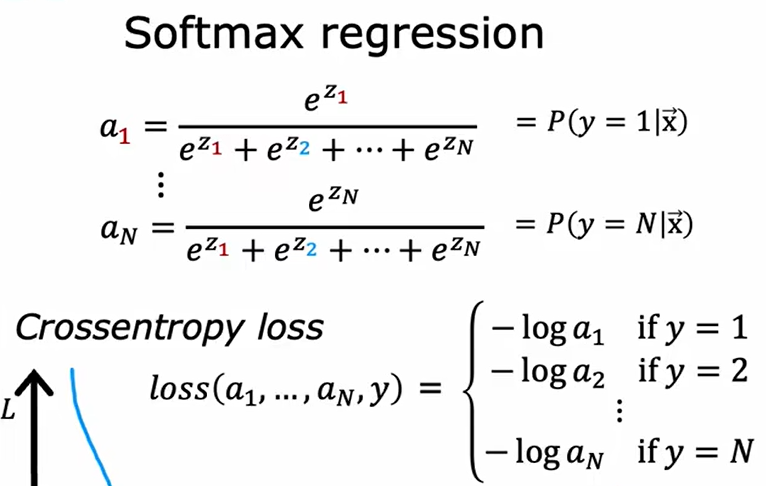
2、优化方式
- 将多步运算合为一步防止中间步带了的误差
- 通过Adam方式加快梯度下降的进度
- 卷积网络，卷积层的每一个单元不使用上一层的所有输入，只用一部分
3、迁移学习
如图像处理等工作，如果样本量较少或者项目周期较短，可以通过使用其他项目的神经网络进行迁移学习：
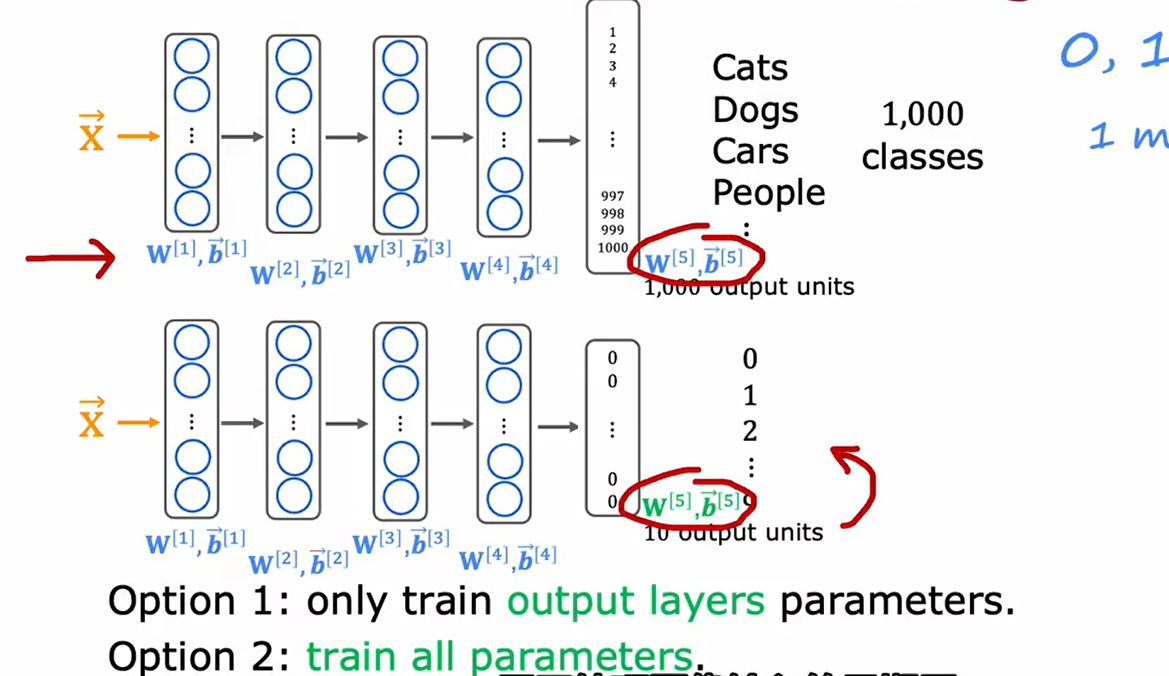
- 方式一：重新训练输出层。
- 方式二：以迁移模型为初始值，重新训练所有参数。
三、模型评估
1、模型的形成、选择与评估
当我们需要在多个模型中选择一个最佳模型，并对其进行评判时，一般我们会将数据集拆分为两份，即train data和test data。二者分别用于训练和测试，最终使用test model的测试结果，如代价函数来评判一个模型的优劣性，然而这是不正确的。
由于test data在多个model中选出的结果最佳的一个，如下例：
虽然w、b参数都是有train data决定的，但参数d是由test data决定的，因此我们不能使用test data作为模型评估的最终结果。
一般来说，工作者会以6:2:2的方式分割元数据集，并将其分为三份：
- training set （训练集）用于训练的过程
- cross validation （交叉验证集） 用于选出最佳的模型
- test set （测试集合） 用于最终进行性能测试
以线性回归为例，三者均使用如下公式进行计算：
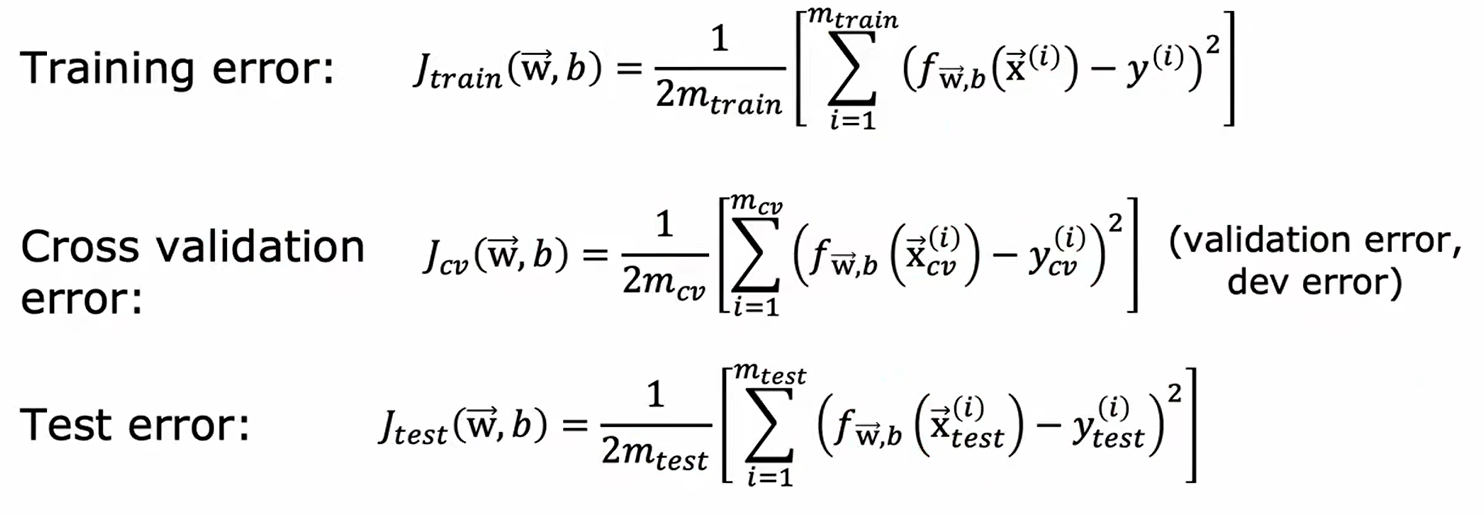
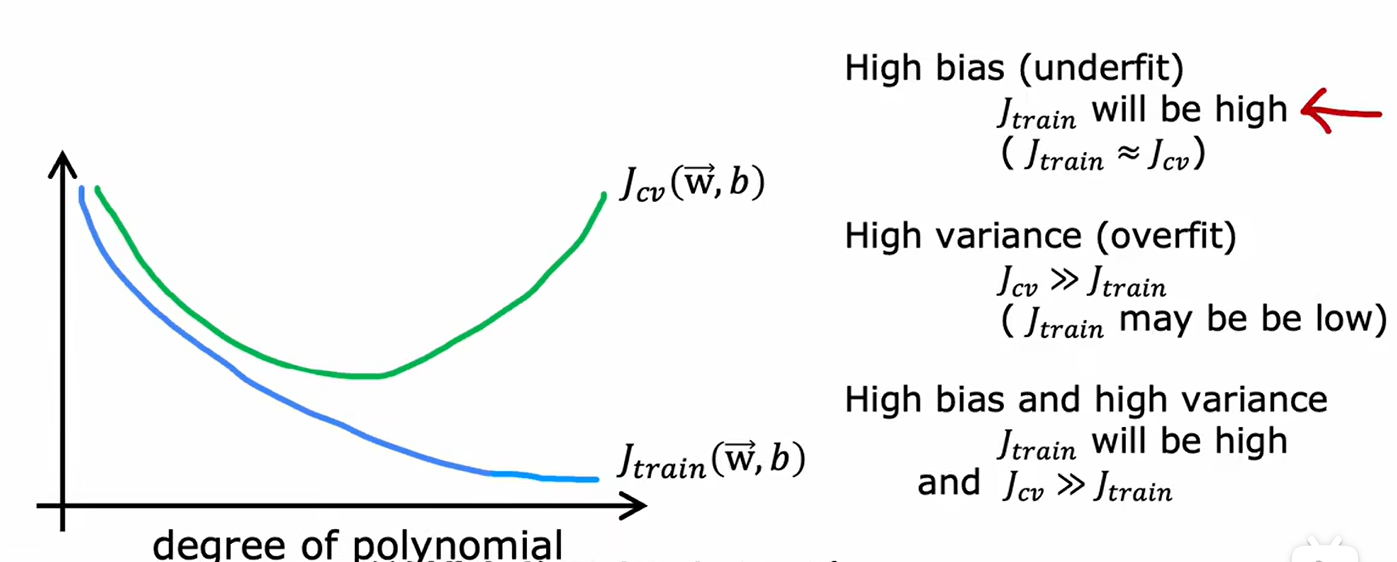
2、方差与偏差
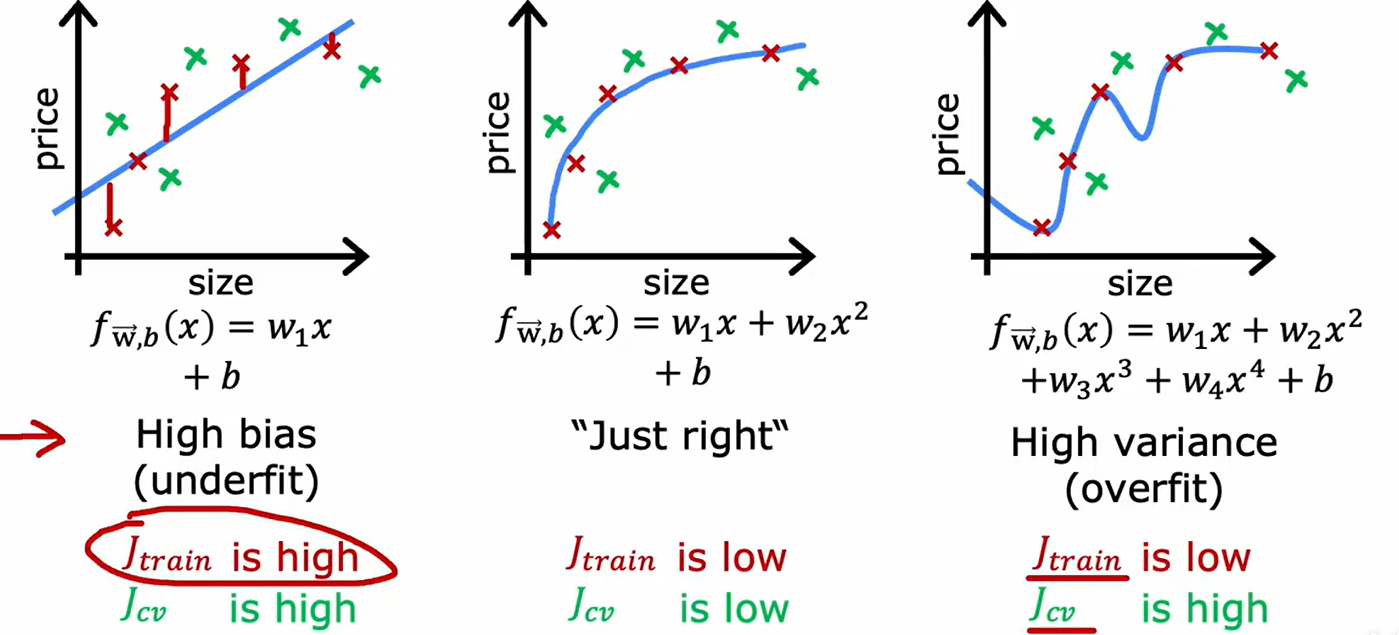
如上图，图左为欠拟合（高偏差）的实例，表现为训练集的损失大、交叉验证集的损失也大；图右为过拟合（高方差）的实例，表现为训练集的损失小，交叉验证集的损失大。由此，我们可以得知如下图所示，随着多项式指数的增加，训练集和交叉验证集的损失函数如下所示：
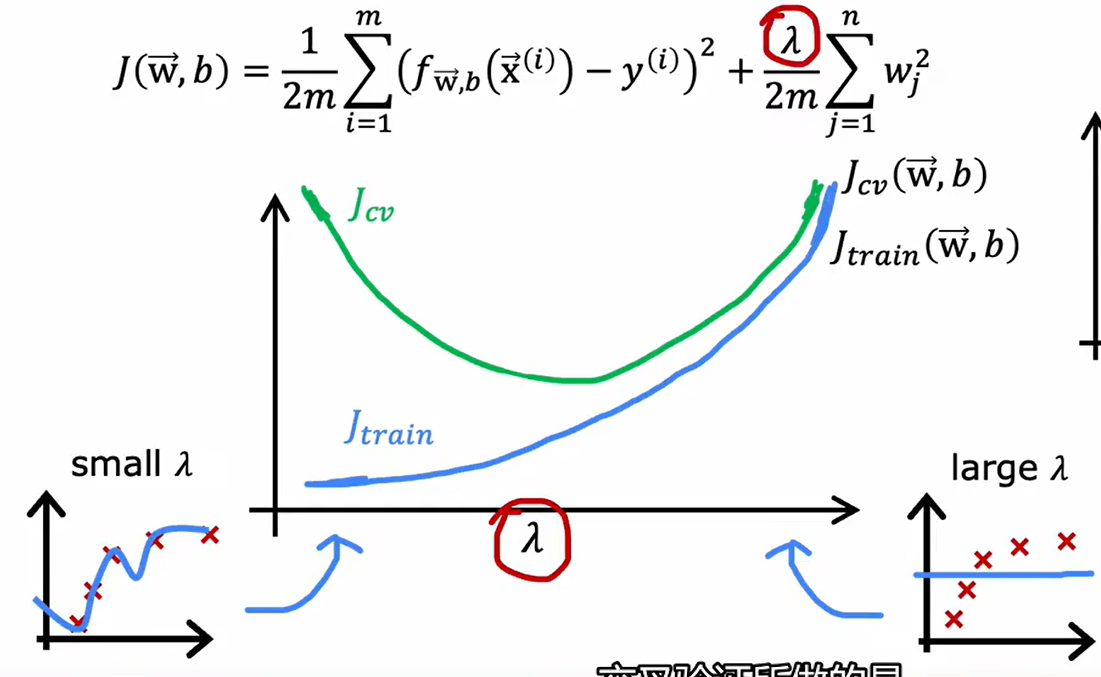
正则化参数对方差偏差的影响如下：
关于调整参数，能为模型带来什么：
- 获取更多训练集 -> 降低偏差
- 减少特征数量 -> 降低偏差
- 添加特征或添加多项式系数 -> 降低方差
- 升高正则化参数 -> 降低偏差
- 降低正则化参数 -> 降低方差
3、精确率和召回率
精确率和召回率的存在是起源于如下问题：
若有一个样本集，其中99%为1，只有1%为0。对应的，一个机器学习程序的内容实际是print(“1”)，则这个模型就能够达到99%的准确度。这样的衡量指标显然是不科学的，而为了解决这一问题，在逻辑回归中，我们不仅仅使用简单的对或错来评判预测结果，而是使用如下方式：
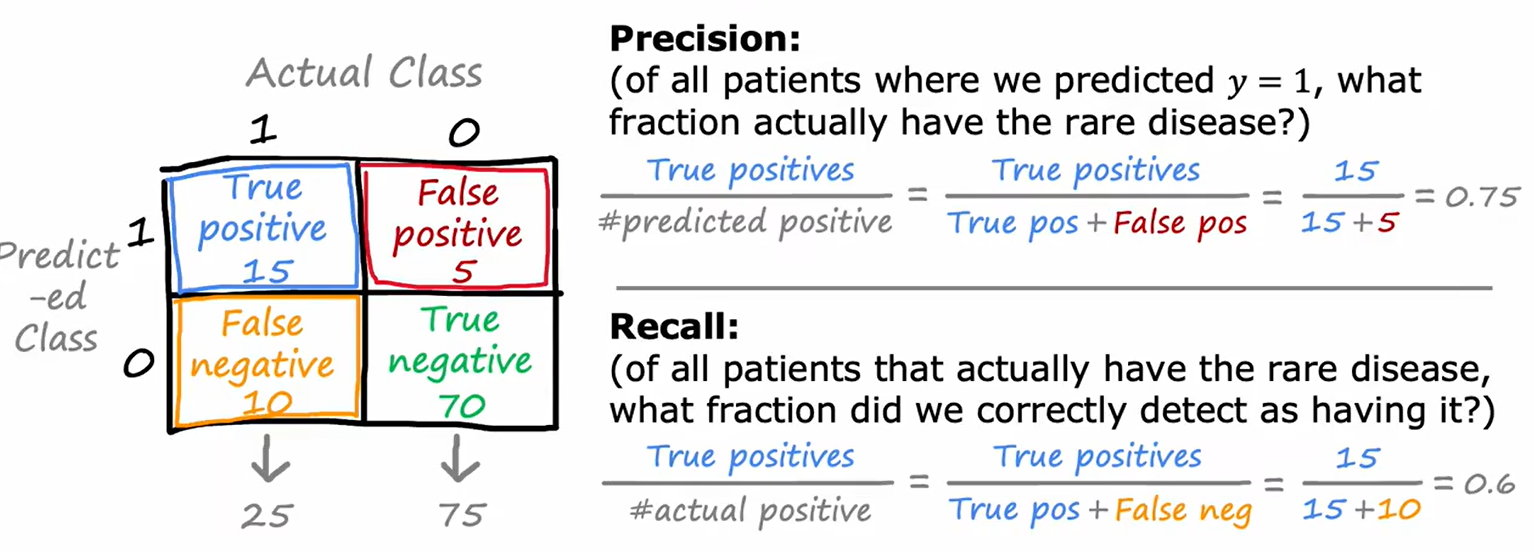
如上图所示：精度（Precision）指向在所有评估为1的结果中正确的比例；而召回率表示在所有为1的结果中，有多少内容被预测出。主观上讲，精确率表示预测的结果的准确程度（即预测的是否对），而召回率表示预测范围的准确程度（即预测的是否全）。
有了如上两个判定方式之后，我们就需要对结果进行评判，我们所希望的是精度和召回率都保持在一定的高度，否则程序就有可能是类似于pirnt(“1”)或print(“0”)的废物程序，因此，可通过如下算式将两个值拟合：
平均值显然是不科学的，通过右下式子的拟合可以保证拟合结果受较小的值较大影响。
四、决策树
要实现二分类文体，也可通过决策树：
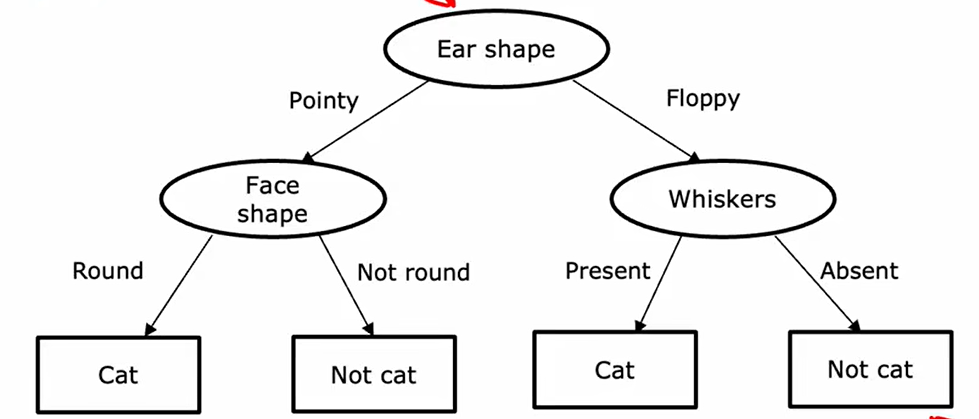
如图所示，每个特征对应一个非叶节点，而叶节点对应决策树的判别结果。输入一个待判断节点时，依次从决策树由上向下归类即可。
1、 决策树基本搭建思路
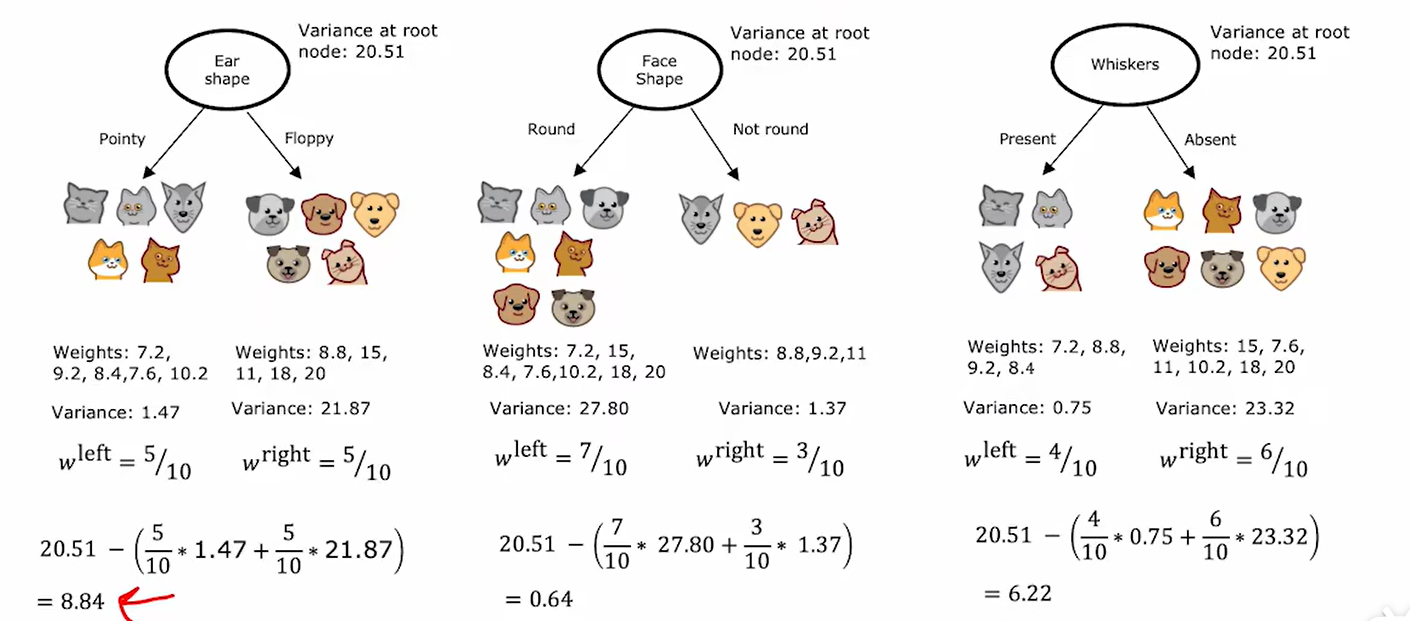
问题一：如何选择在哪一个节点使用哪一个特征进行分类？
和信息像是，决策树在每个节点尽量减少熵，即增大纯度（也就是尽量分的更加正确，尽量一边全是猫、一边全是狗）。
那么下面给出如何衡量纯度：
首先我们需要学会如何计算熵：
熵是衡量纯度的唯一标准，若一组数据熵比较大，则说明纯度小；反之熵小则说明纯度大。而熵是可以和比例相互对应的，比例越接近1：1，则说明熵越大。如下图，横轴为比例，纵轴为熵：
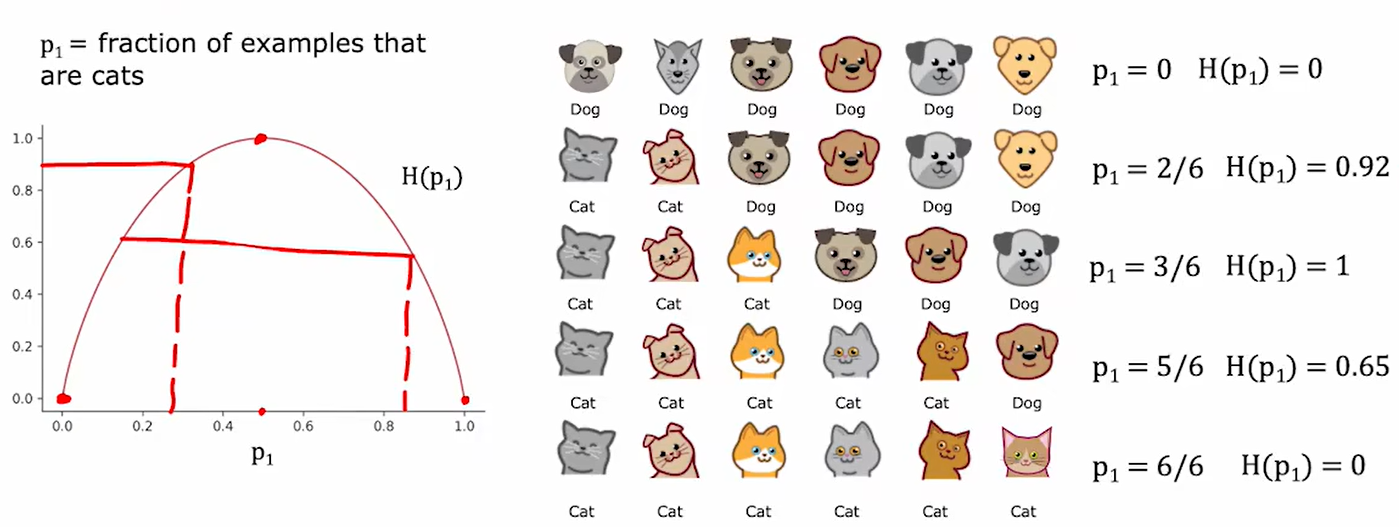
下面是计算熵的公式：
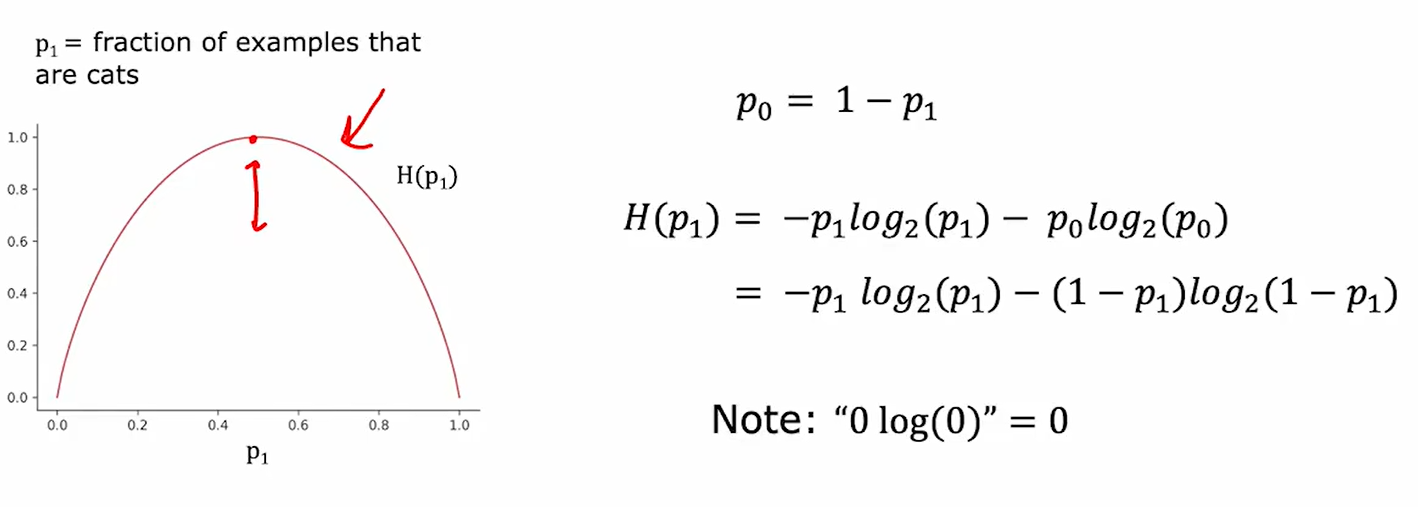
综上，只要给出任意一个节点的样本数据，我们就可以给出他的熵。
然后，学会计算一组样本的熵后，可如下计算纯度的增益（信息增益）：
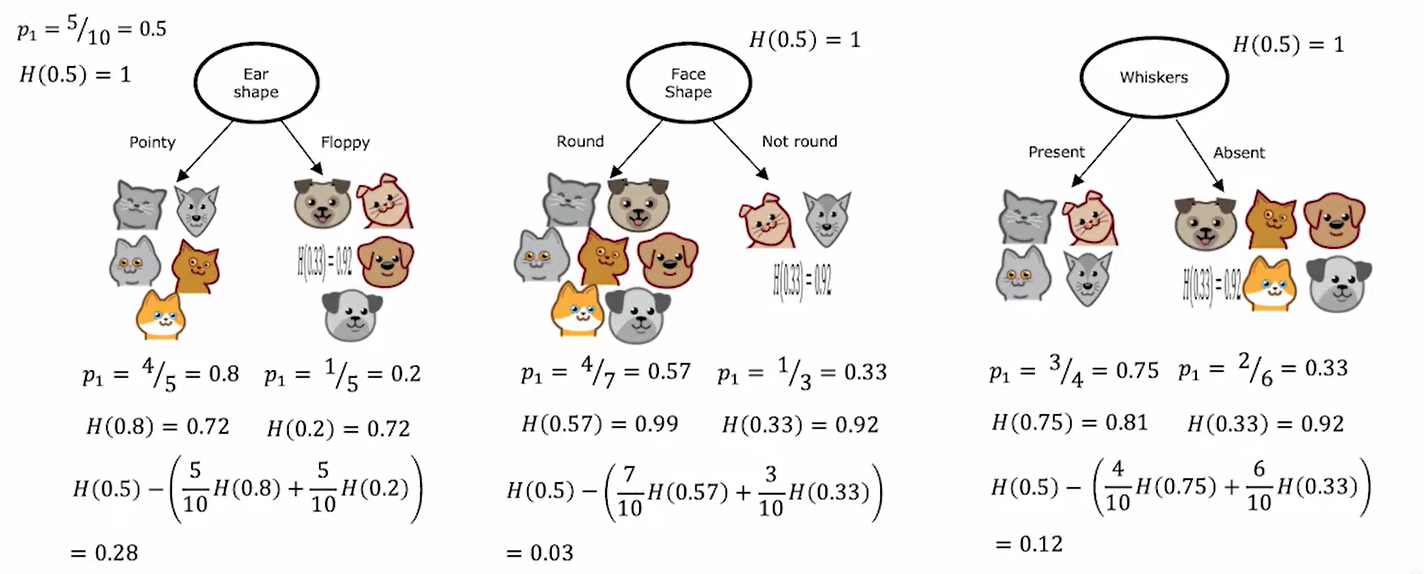
上式可以表示为：
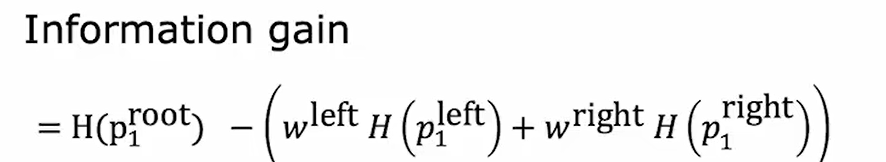
如上，计算了从上一步到下一步减少熵最多的，也就是纯度上升（信息增益）最大的。
问题二：合适停止对节点进行继续分类？
- 当一个节点成为只有一种样本的节点，则不继续拆分；
- 当分裂已经超过了树的最大深度（根节点为0），则不继续拆分；若树太大，可能过拟合
- 若继续拆分节点导致的纯度的上升的程度低于阈值，则不继续拆分；
- 若某个节点的样本数低于阈值，则不继续拆分；
2、one-hot编码
当特征不只有两个可能性时，可以将其按照如下的方式转化：
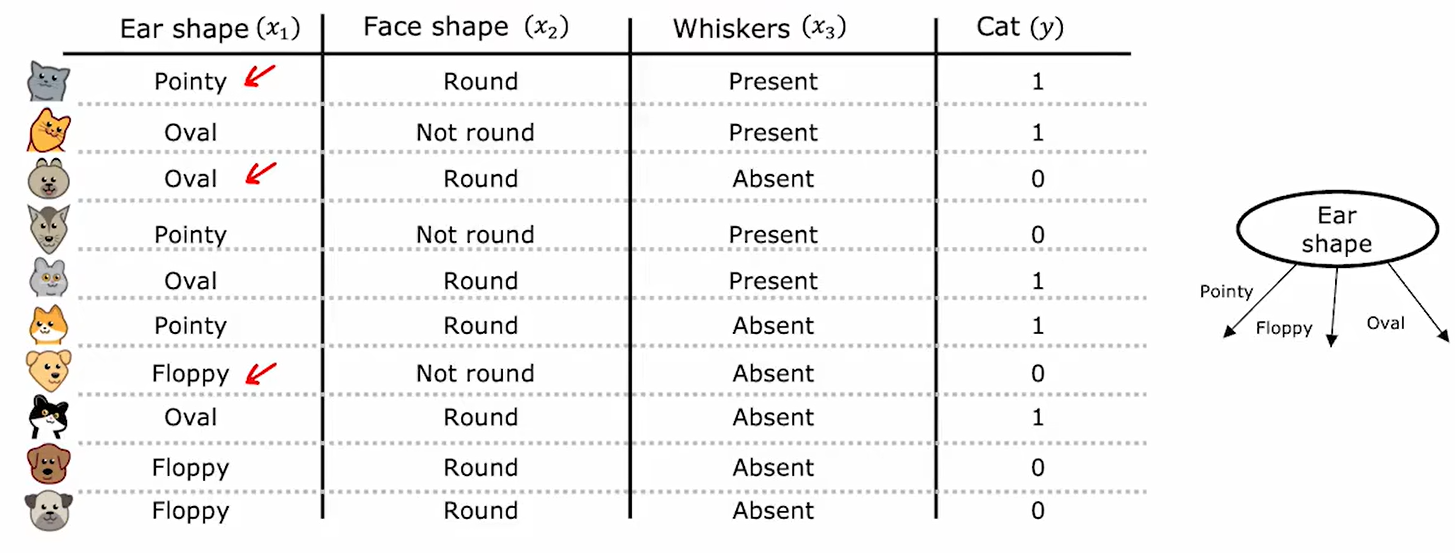
如上图，耳朵特征有三种可能的取值，因此可转化为如下：
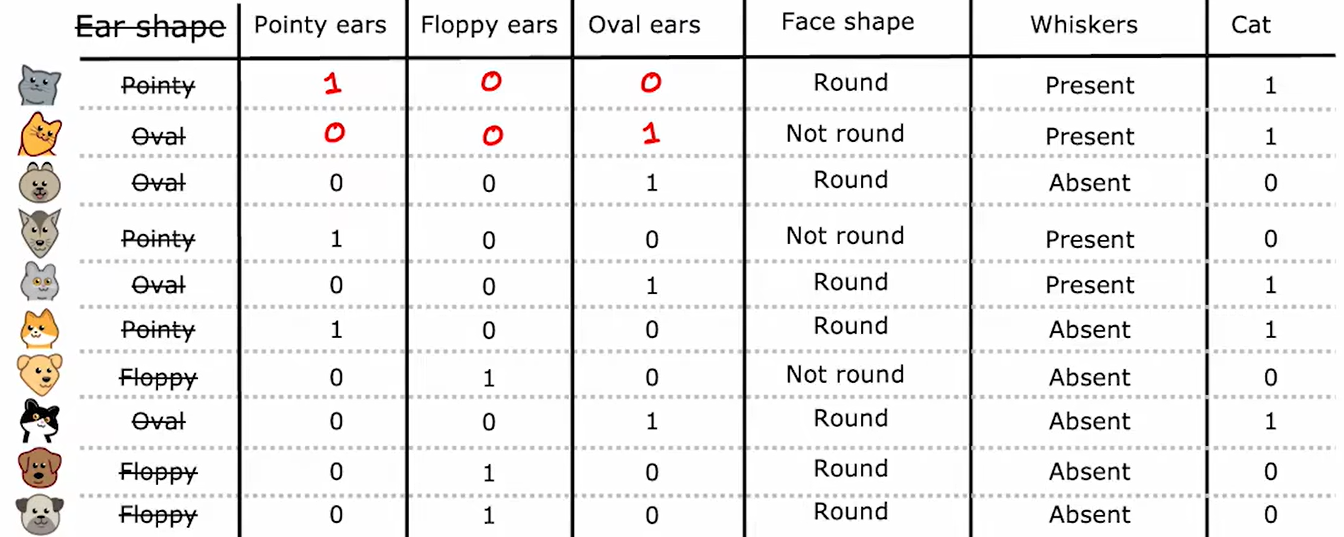
将一个特征放缩为三个特征，即可继续使用二分类。综上，对于一个有k种可能的特征，可将其放缩为k个特征，同一样本的这k个特征中，一定有且只有一个为1。
3、连续有价值特征
当二分类问题中有如下具体数字（weight），而非离散的特征时，可以使用熵将其划分为二分离散特征。
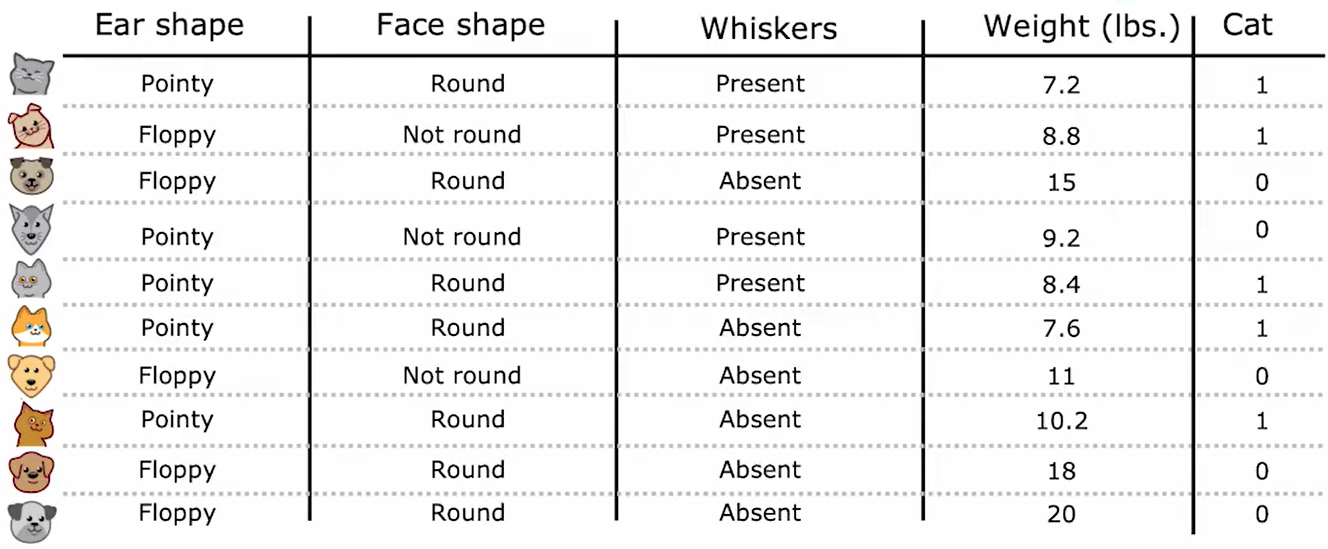
如图所示，可通过不断尝试划分情啊坤哥，来确定信息增益最大的划分方式：
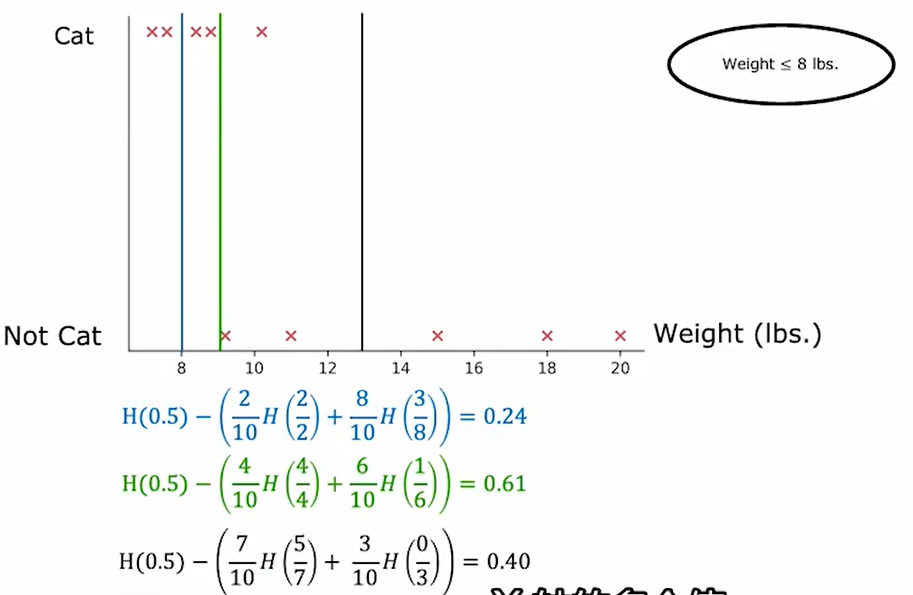
如上图，选择weight=9 ，也就是绿的划分方式增益最大，因此直接将weight是否小于9作为一个特征就可以了。（上式中的比例系数时正样本在所有样本中所占的比例）
4、回归树
当希望决策树不仅能预测离散的二分情况，而是能预测数值时，可以使用回归树。其核心思想与决策树相同，只是使用反差来衡量熵的减小情况，入下图：
5、决策森林
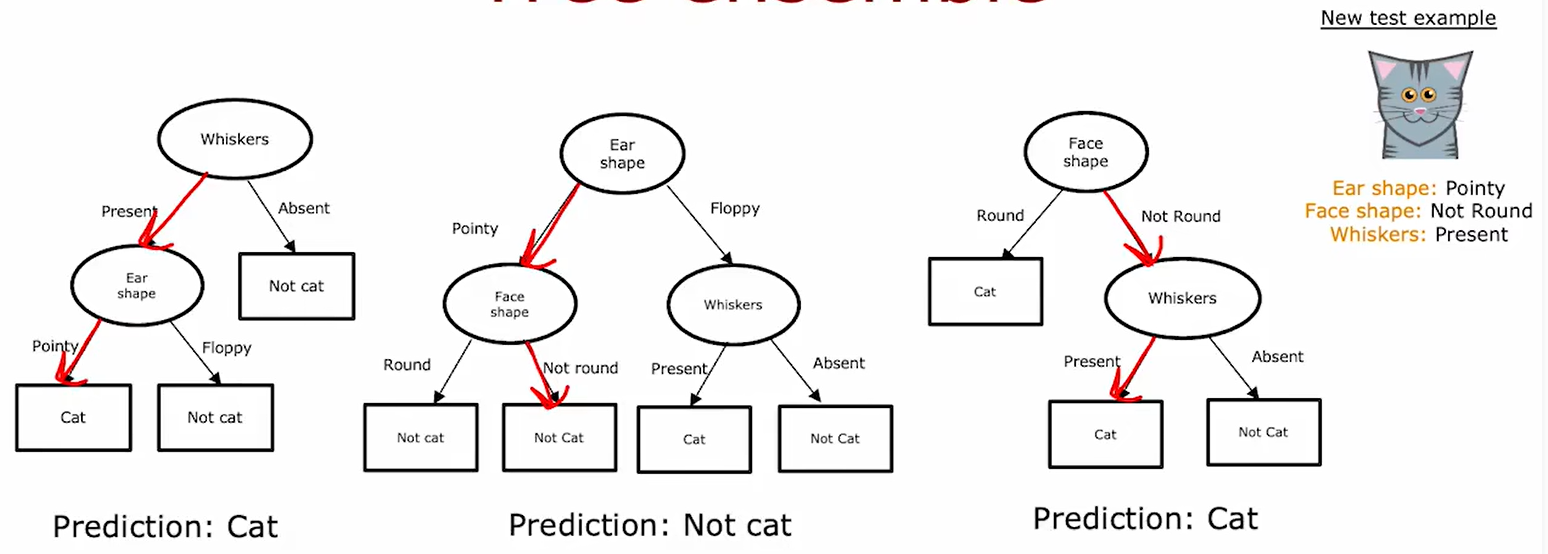
决策森林的存在用于解决决策树的不健壮问题。不健壮，指决策树训练集的微小变化可能导致决策树的巨幅改变。
我们可以构建多个决策树（决策森林），通过多个决策树（决策森林）分别判断结果后进行投票，最终区票数高的结果即可：
根据上上述对于决策树构建过程的叙述，对于同一组样本，决策树的产生是唯一的，因此可以使用有放回抽样的方式，构造伪随机样本集。 有放回抽样，就是在n个样本中抽n次，每次抽完后记录结果并放回。
即使使用了上述方法构造有放回抽样的随机森林，决策森林也有可能出现节点顺序、结构依然相似的情况。此时可以在生成新节点时不用所有特征进行判定比较，而是在n个特征中选择其子集（假设包含k个特征）进行对于节点特征的选取工作，当n较大，一般k取n的平方根。
以上方式，都是构建决策森林的方式，同样的，有一种决策森林构建法叫做xgboosting
6、XGBoost
XGBoost的核心思想是，构建新的决策树时，提高上一个决策树判断错误的样本出现的频率。
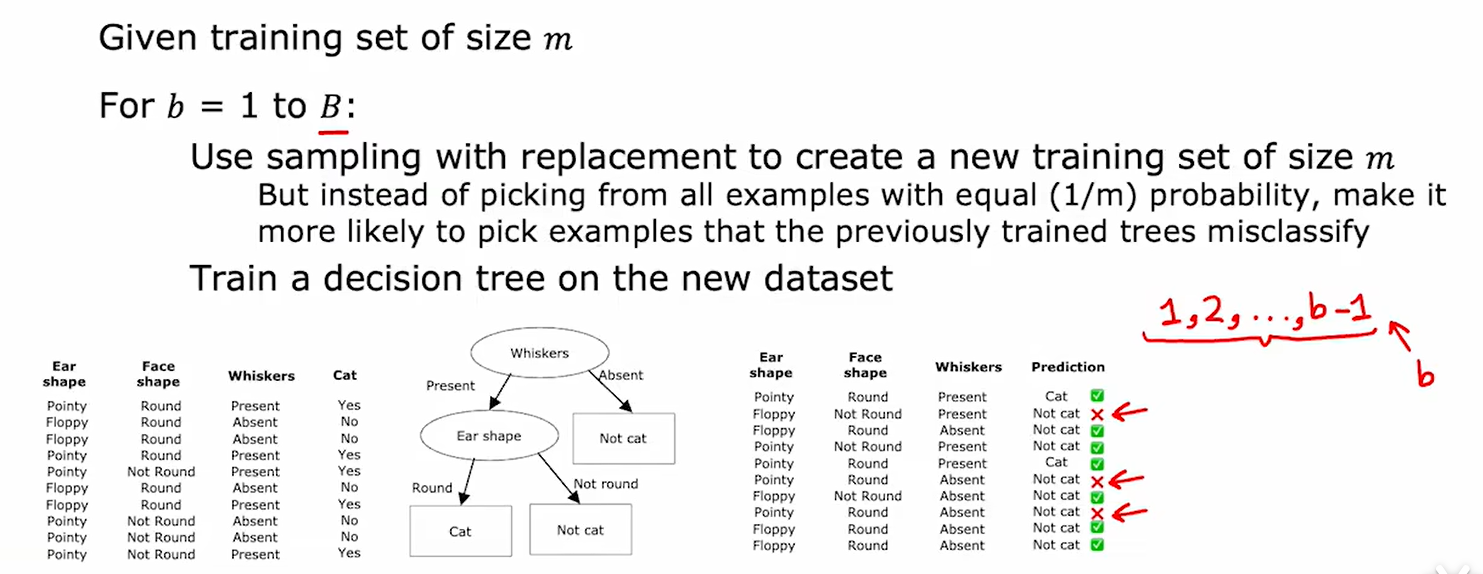
如上所示，假设第b-1个决策树如图所示，其中有三个样本判断错误，就应在构建第b棵决策树时提高这三个样本出现的概率。
更多细节没讲，可以使用 from xgboost import XGBClassifier 来使用这一模型
7、决策树&神经网络
