reverse_花指令实例

以看雪.TSRC 2017CTF秋季赛第二题为例，解决花指令的反调试问题。

image-20220305101852053

一上来就F5失败。

一开始先打印了一行字，然后调用了一个干扰函数，进入逻辑相对清晰的sub_401050:

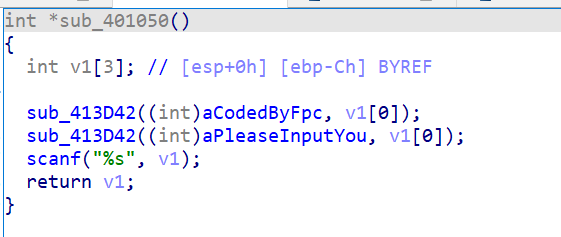
image-20220305102332825

scanf()没限制长度，可以把返回地址盖掉。。。

所以说，基础的逻辑都是假的，这题就是要输入一个比较长的内容覆盖返回地址后才会出现真东西。

那么，我们要跳到哪里才能正常执行呢？

idaview往下找：

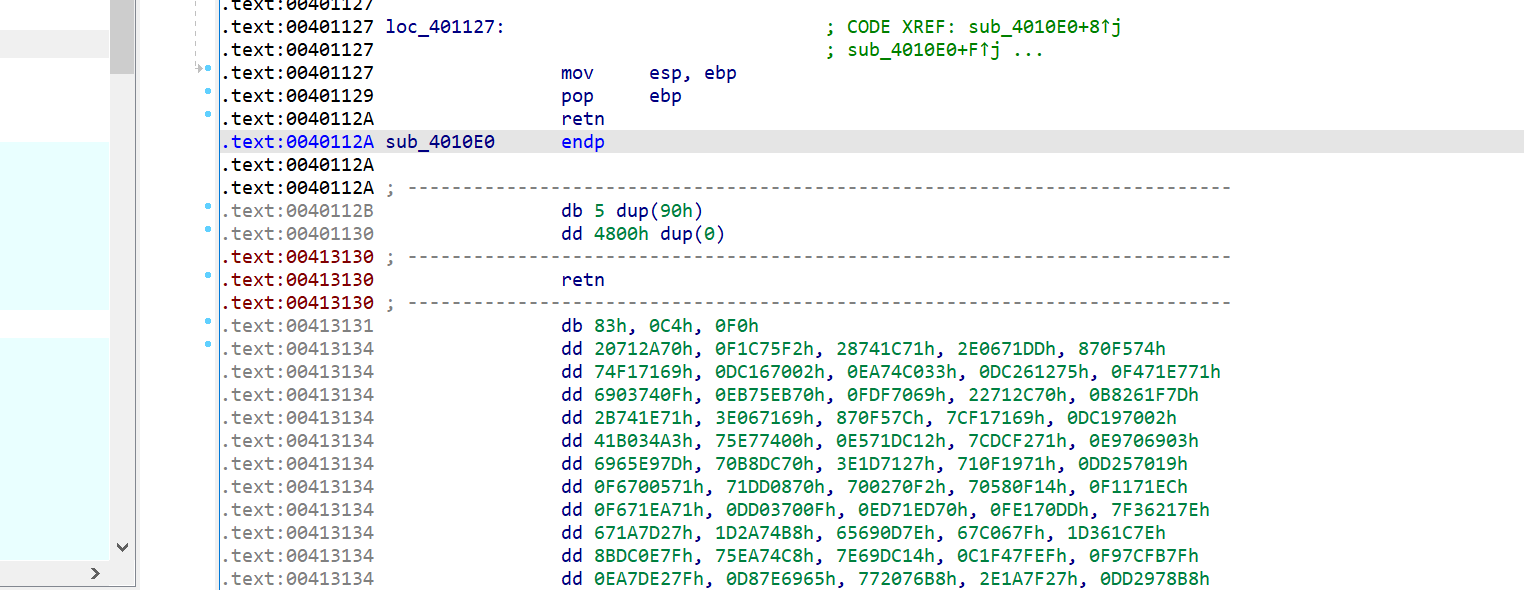
image-20220305103253955

c键变code：

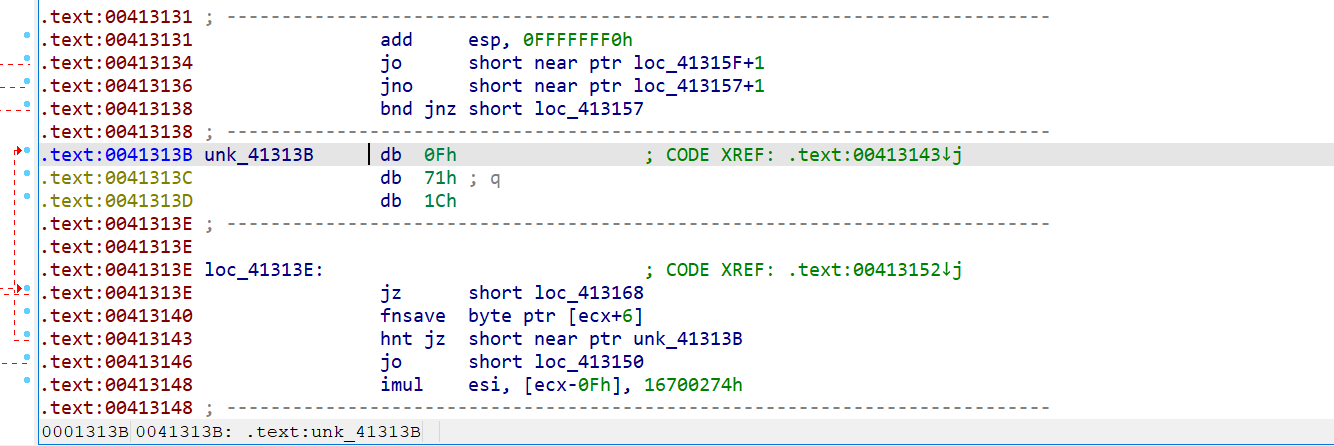
image-20220305103327310

看起来比较靠谱，也就是说应该跳转到地址0x00413131处。

我们可以直接pwn-tools构造一个脚本，但似乎听说看雪比赛似乎是只能输入字母和数字的，仔细看地址正好是A11的值，因此就不需要折磨自己了。

直接构造溢出字符串为222222222222A11(十二个填充位，三个溢出地址位)。

扔进去执行，并没有什么变化。。。动调看看吧。。

image-20220305103952383

进来先整一个断点，然后直接F9

发现我傻了，地址构造反了，正确的应该是22222222222211A（小端序）

同样动调，然后remove analysis from this module，把这里变回代码。

然后动调发现绕来绕去，快疯了，这里记录一个：

调试跟踪跳转多的技巧

view-Run trace打开跟踪窗口，ctrl-F11为记录步入后的逻辑，ctrl-F12为记录步过的逻辑，就相当于记录了手动F7/f8运行的每一步逻辑，都可以在窗口中查看，这一样就会在跳转非常多的情况下清晰的多。

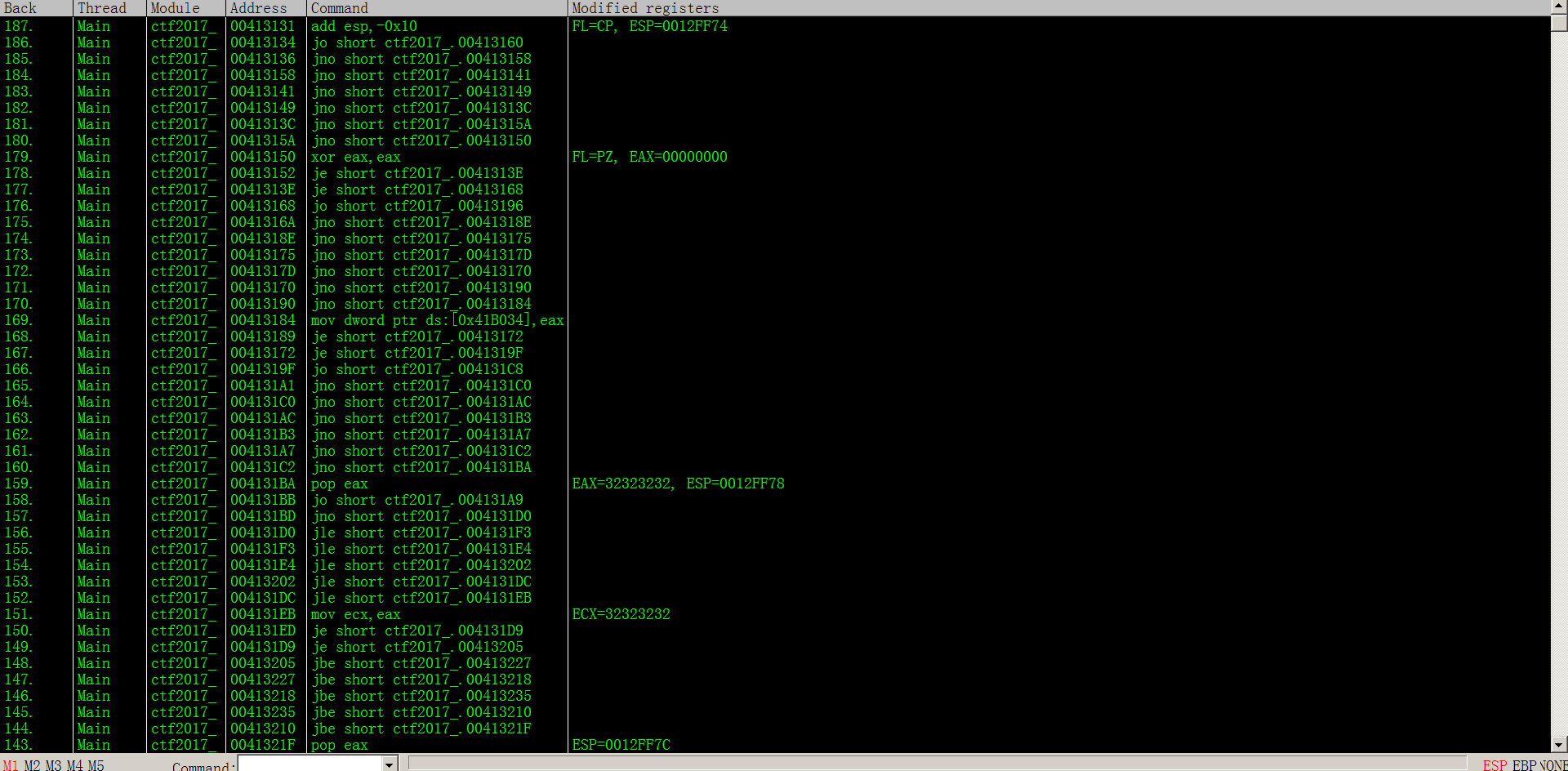
image-20220305114920532

这样就清晰的多了，然后我就不会了。。。

以下参考：https://bbs.pediy.com/thread-222284.htm（真是恐怖）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
//还原的加花乱序
////////////////////////////////////////
 add esp,-0x10
 xor eax,eax
 mov dword ptr ds:[0x41B034],eax
 
 pop eax        //eax=x
 mov ecx,eax    //ecx=x
 
 pop eax        //eax=y
 mov ebx,eax    //ebx=y
 
 pop eax        //eax=z
 mov edx,eax    //edx=z
 
 mov edx,eax   
 mov eax,ecx    //eax=x
 sub eax,ebx    //eax=x-y
 shl eax,0x2    //eax shl 2
 add eax,ecx    //eax+=x
 add eax,edx    //eax+=z
 sub eax,0xEAF917E2 //(必须为零)
 
 add eax, ecx    //eax=x
 sub eax, ebx    //eax-=y
 mov ebx, eax    //ebx=(x-y)
 shl eax, 1        //eax shl 1
 add eax, ebx    //eax+=(x-y)
 add eax, ecx    //eax+=x
 mov ecx, eax    //ecx=eax
 add eax, edx    //eax+=edx
 sub eax, 0xe8f508c8 //(必须为零)
 
 mov eax, ecx    //eax=original
 mov eax, ecx
 sub eax, edx    //eax-=edx
 sub eax, 0xc0a3c68 //(必须为零)
 
 pop eax
 xor eax, 0x8101
 mov edi, eax
 xor eax, eax
 stosd dword ptr es:[edi], eax
 call 0x413841  //00413830 PUSH 00413835
 pop eax
 push eax
 mov edi, eax
 mov edi, eax
 push 0x4e000969
 pop eax
 xor eax, edx
 stosd dword ptr es:[edi], eax
 xor eax, 0x10a3e
 stosd dword ptr es:[edi], eax
 xor eax, ebx
 xor eax, 0x22511e14
 stosd dword ptr es:[edi], eax
 xor eax, 0x61642d
 xor eax, dword ptr [0x41b034]
 jmp eax
 ////////////////////////////////////////////

大哥硬是把逻辑整理出来了。。。恐怖如斯，我不能理解

然后就是根据三个为零条件求解三元方程。。。，这里依然搬运一下：

((x-y) shl 2)+x+z==0xEAF917E2 即3942193122‬
(x-y) shl 1 + (x-y) +x+z==0xe8f508c8 即3908372680
(x-y) shl 1 + (x-y) +x-z==0xc0a3c68 即201997416

反正总之最后解出来了，然后转化为字符串就是答案。。。